4.3.7 Приведение кривой второго порядка к каноническому виду

Уравнение второго порядка вида

определяет на плоскости кривую. Группа членов называется квадратичной формой, – линейной формой. Если в квадратичной форме содержатся только квадраты переменных, то такой ее вид называется каноническим, а векторы ортонормированного базиса, в котором квадратичная форма имеет канонический вид, называются главными осями квадратичной формы.

Матрица 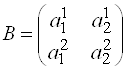называется матрицей квадратичной формы. Здесь . Чтобы матрицу привести к диагональному виду, необходимо за базис взять собственные векторы этой матрицы, тогда , где и – собственные числа матрицы .

В базисе из собственных векторов матрицы квадратичная форма будет иметь канонический вид: .

Эта операция соответствует повороту осей координат. Затем производится сдвиг начала координат, избавляясь тем самым от линейной формы.

Канонический вид кривой второго порядка: , причем:

А) если – эллипс, в частности, при это окружность;

Б) если имеем гиперболу;

В) если либо , то кривая является параболой и после поворота осей координат имеет вид (здесь ). Дополняя до полного квадрата, будем иметь: .

Пример 14. Дано уравнение кривой

в системе координат , где и .

1. Определить тип кривой.

2. Привести уравнение к каноническому виду и построить кривую в исходной системе координат.

3. Найти соответствующие преобразования координат.

Решение. Приводим квадратичную форму к главным осям, то есть к каноническому виду. Матрица этой квадратичной формы 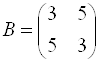. Находим собственные числа и собственные векторы этой матрицы:

Характеристическое уравнение:

; . Вид квадратичной формы: .

Исходное уравнение определяет гиперболу.

Заметим, что вид квадратичной формы неоднозначен. Можно записать , однако тип кривой остался тот же – гипербола.

Находим главные оси квадратичной формы, то есть собственные векторы матрицы . .

Собственный вектор, отвечающий числу при : .

В качестве единичного собственного вектора принимаем вектор 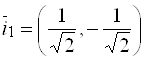, где – длина вектора .

Координаты второго собственного вектора, соответствующего второму собственному числу , находим из системы

.

; .

Итак, имеем новый ортонормированный базис .

По формулам (5) пункта 4.3.3. переходим к новому базису:

или

; . (*)

Вносим выражения и в исходное уравнение и, после преобразований, получаем: .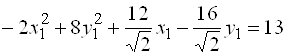

Выделяем полные квадраты: .

Проводим параллельный перенос осей координат в новое начало: , .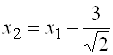

Если внести эти соотношения в (*) и разрешить эти равенства относительно и , то получим: , 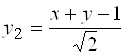. В системе координат данное уравнение имеет вид: .

Для построения кривой строим в старой системе координат новую: ось задается в старой системе координат уравнением , а ось уравнением . Начало новой системы координат является точкой пересечения этих прямых.

Для упрощения восприятия разобьем процесс построения графика на 2 этапа:

1. Переход к системе координат с осями , заданными в старой системе координат уравнениями и Соответственно.

2. Построение в полученной системе координат графика функции.

Окончательный вариант графика выглядит следующим образом

Аналогично можно упростить, то есть привести к каноническому виду, поверхность второго порядка.

Для самостоятельной работы.

1. Оператор в пространстве действует по закону .

А) Доказать, что вектор является собственным вектором оператора . Найти его собственное число.

Б) Привести матрицу оператора к диагональному виду путем перехода к новому базису. Найти этот базис и соответствующую ему матрицу.

Ответ: ; ; .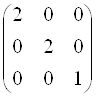

2. Доказать, что матрица к диагональному виду не приводится.

3. Даны уравнения кривых:

А) ;

Б) ;

В) .

Определить тип кривых; кривую а) построить.

Ответ: а) эллипс; б) парабола; в) гипербола.

< Предыдущая		Следующая >