4.3.6 Собственные числа и собственные векторы линейного оператора

Наиболее просто устроены матрицы диагонального вида . Возникает вопрос, нельзя ли найти базис, в котором матрица линейного оператора имела бы диагональный вид. Такой базис существует.

Пусть дано линейное пространство и действующий в нем линейный оператор ; в этом случае оператор переводит в себя, то есть .

Определение. Ненулевой вектор называется собственным вектором оператора , если оператор переводит в коллинеарный ему вектор, то есть . Число называется собственным значением или собственным числом оператора , соответствующим собственному вектору .

Отметим некоторые свойства собственных чисел и собственных векторов.

1. Любая линейная комбинация собственных векторов оператора , отвечающих одному и тому же собственному числу , является собственным вектором с тем же собственным числом.

2. Собственные векторы оператора с попарно различными собственными числами линейно независимы.

3. Если собственные числа , то собственному числу соответствует не более линейно независимых собственных векторов.

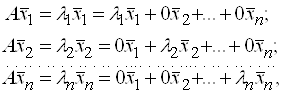Итак, если имеется линейно независимых собственных векторов , соответствующих различным собственным числам , то они линейно независимы, следовательно, их можно принять за базис пространства . Найдем вид матрицы линейного оператора в базисе из его собственных векторов, для чего подействуем оператором на базисные векторы: тогда .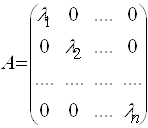

Таким образом, матрица линейного оператора в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора .

Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.

Теорема. Матрица линейного оператора в базисе имеет диагональный вид тогда и только тогда, когда все векторы базиса – собственные векторы оператора .

Правило отыскания собственных чисел и собственных векторов.

Пусть дан вектор , где – координаты вектора относительно базиса и – собственный вектор линейного оператора , соответствующий собственному числу , то есть . Это соотношение можно записать в матричной форме

. (*)

Уравнение (*) можно рассматривать как уравнение для отыскания , причем , то есть нас интересуют нетривиальные решения, поскольку собственный вектор не может быть нулевым. Известно, что нетривиальные решения однородной системы линейных уравнений существуют тогда и только тогда, когда . Таким образом, для того, чтобы было собственным числом оператора необходимо и достаточно, чтобы .

Если уравнение (*) расписать подробно в координатной форме, то получим систему линейных однородных уравнений:

(1)

Где – матрица линейного оператора.

Система (1) имеет ненулевое решение, если ее определитель равен нулю

.

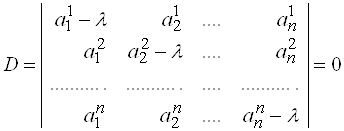Получили уравнение для нахождения собственных чисел.

Это уравнение называется характеристическим уравнением, а его левая часть – характеристическим многочленом матрицы (оператора) . Если характеристический многочлен не имеет вещественных корней, то матрица не имеет собственных векторов и ее нельзя привести к диагональному виду.

Пусть – вещественные корни характеристического уравнения, причем среди них могут быть и кратные. Подставляя по очереди эти значения в систему (1), находим собственные векторы.

Пример 12. Линейный оператор действует в по закону , где – координаты вектора в базисе , , . Найти собственные числа и собственные векторы этого оператора.

Решение. Строим матрицу этого оператора:

.

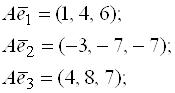
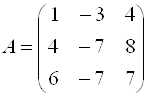Составляем систему для определения координат собственных векторов:

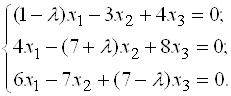
Составляем характеристическое уравнение и решаем его:

.

.

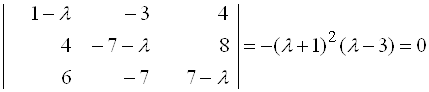Подставляя в систему, имеем:

или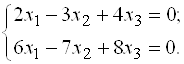

Так как 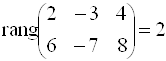, то зависимых переменных два, а свободное одно.

Пусть – свободное неизвестное, тогда 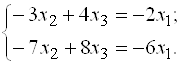Решаем эту систему любым способом и находим общее решение этой системы: Фундаментальная система решений состоит из одного решения, так как .

Множество собственных векторов, отвечающих собственному числу , имеет вид: , где – любое число, отличное от нуля. Выберем из этого множества один вектор, например, положив : .

Рассуждая аналогично, находим собственный вектор, отвечающий собственному числу : .

В пространстве базис состоит из трех линейно независимых векторов, мы же получили только два линейно независимых собственных вектора, из которых базис в составить нельзя. Следовательно, матрицу линейного оператора привести к диагональному виду не можем.

Пример 13. Дана матрица .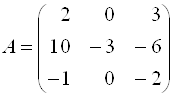

1. Доказать, что вектор является собственным вектором матрицы . Найти собственное число, соответствующее этому собственному вектору.

2. Найти базис, в котором матрица имеет диагональный вид.

Решение.

1. Если , то – собственный вектор

.

Вектор – собственный вектор. Собственное число .

Диагональный вид матрица имеет в базисе, состоящем из собственных векторов. Один из них известен. Найдем остальные.

Собственные векторы ищем из системы:

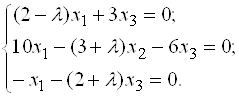
Характеристическое уравнение: ;

; ;

.

Найдем собственный вектор, отвечающий собственному числу :

Ранг матрицы этой системы равен двум и равен числу неизвестных, поэтому эта система имеет только нулевое решение . здесь может быть любым, отличным от нуля, например, . Таким образом, вектор является собственным вектором, отвечающим . Проверим:

.

Если , то получаем систему

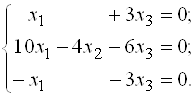
Ранг матрицы равен двум. Последнее уравнение вычеркиваем.

Пусть – свободное неизвестное. Тогда , , .

Полагая , имеем – собственный вектор, отвечающий собственному числу . Проверка:

.

Так как собственные числа действительные и различны, то векторы, им отвечающие, линейно независимы, поэтому их можно принять за базис в . Таким образом, в базисе , , матрица имеет вид:

.

Не всякую матрицу линейного оператора можно привести к диагональному виду, поскольку для некоторых линейных операторов линейно независимых собственных векторов может быть меньше . Однако, если матрица симметрическая, то корню характеристического уравнения кратности соответствует ровно линейно независимых векторов.

Определение. Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой .

Замечания. 1. Все собственные числа симметрической матрицы вещественны.

2. Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.

В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.

< Предыдущая		Следующая >