4.3.5 Линейный оператор и его матрица

Определение. Пусть даны два пространства и . Если по закону каждому вектору поставлен в соответствие вектор , то говорят, что задан оператор (функция, отображение), отображающий в и пишут .

Обозначение: ; – образ, – прообраз.

Определение. Если для любых и из и любых вещественных чисел и имеет место , то оператор называется линейным.

Произвольные отображения линейных пространств изучаются в курсе математического анализа. В курсе линейной алгебры изучаются лишь линейные отображения.

Пример 6. Оператор действует из в по закону , где , и – фиксированный вектор, например, . Оператор переводит вектор из в другой вектор из . Докажем, что он линейный: . Здесь воспользовались свойствами векторного произведения.

Пример 7. Линеен ли оператор , где произвольный вектор, а вектор – фиксированный?

Решение. , так как , . Следовательно, оператор – нелинейный.

Пусть даны два пространства и и оператор , действующий из в . Пусть в есть базис , а в – базис .

Подействовав оператором на базисные векторы пространства , получим векторы из , которые можно разложить по базису с коэффициентами линейных комбинаций :

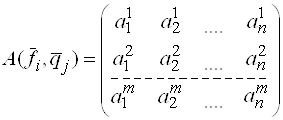
Строим матрицу таким образом, чтобы в ее столбцах стояли координаты образов базисных векторов пространства относительно базисных векторов пространства :

.

Матрица называется матрицей линейного оператора , действующего из в . Таким образом, если оператор , то матрица этого оператора имеет размер , то есть у нее строк и столбцов.

Замечание. Если в и выбрать другие базисы, то в этих базисах матрица линейного оператора будет иметь другой вид.

Из определения матрицы линейного оператора следует, что, зная закон (оператор), по которому вектору сопоставляется вектор , можно построить матрицу, и наоборот, любой матрице соответствует некоторый линейный оператор.

Пример 8. Построить матрицу линейного оператора, действующего из в по закону , где векторы и заданы относительно канонического базиса.

Решение. Подействуем оператором на базисные векторы :

;

;

.

Таким, образом, – искомая матрица.

Пример 9. Пусть в выбран базис , , , а в выбран базис , . Найти матрицу линейного оператора, действующего из в по закону , где .

Решение. ; ;

; .

Пример 10. Дана матрица . Найти линейный оператор (закон, по которому действует оператор).

Решение. Матрица – это матрица линейного оператора, действующего из в . Пусть в базис , в базис . Так как в столбцах матрицы стоят координаты векторов относительно базиса , то

(1)

Пусть произвольный вектор из , где – координаты этого вектора в базисе , тогда . Действуя оператором на вектор и учитывая линейность оператора, получим: .

Учитывая (1), имеем:

.

Таким образом, оператор действует по закону

.

Зная матрицу оператора , результат его действия на вектор можно найти в матричной форме. Пусть известна матрица оператора размера с элементами . В этом случае оператор с такой матрицей действует из в . Если – любой вектор из , то результат действия оператора на вектор можно найти по формуле:

,

Где – координаты вектора .

Пример 11. Операторы и действуют в пространстве по законам , , где ; ( – скалярное произведение векторов и ). Найти координаты вектора в каноническом базисе.

Решение. Координаты вектора можно найти двумя способами:

А) найдем матрицу .

Строим матрицу в каноническом базисе:

; ;

.

.

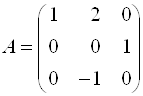Строим матрицу в каноническом базисе:

; ;

.

;

.

.

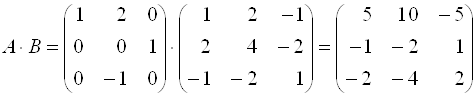Этот способ решения называется матричным;

Б) операторный способ.

. Подействуем оператором на вектор :

, теперь на полученный вектор подействуем оператором :

.

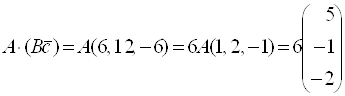Для самостоятельной работы.

1. Оператор действует по закону:

.

Найти его матрицу в каноническом базисе.

Ответ: .

2. Оператор действует в плоскости и осуществляет зеркальное отражение относительно прямой . Доказать, что он линейный и найти его матрицу в каноническом базисе.

Ответ: .

3. Дана матрица .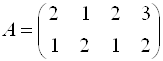

А) Найти оператор, матрицей которого является матрица .

Б) Найти образ вектора .

Ответ: .

< Предыдущая		Следующая >