4.3.4 Евклидовы линейные пространства
Определение. Если в линейном пространстве ![]() введено понятие скалярного произведения векторов, то такое пространство называется евклидовым и обозначается
введено понятие скалярного произведения векторов, то такое пространство называется евклидовым и обозначается ![]() . Евклидово пространство конечномерно.
. Евклидово пространство конечномерно.
Определение. Скалярным произведением двух векторов ![]() и
и ![]() линейного пространства
линейного пространства ![]() называется число, обозначаемое
называется число, обозначаемое ![]() и удовлетворяющее условиям:
и удовлетворяющее условиям:
А) ![]() ;
;
Б) ![]() ;
;
В) ![]() ;
;
Г) ![]() , если
, если ![]() и
и ![]() , если
, если ![]() .
.
В пространстве ![]() скалярное произведение введем следующим образом. Пусть
скалярное произведение введем следующим образом. Пусть ![]() ,
, ![]() – два произвольных вектора из
– два произвольных вектора из ![]() , тогда положим
, тогда положим ![]() (условия «а–г», очевидно, выполнены).
(условия «а–г», очевидно, выполнены).
Определение. Длиной вектора ![]() пространства
пространства ![]() называется число
называется число ![]() .
.
В ![]() длина вектора равна
длина вектора равна ![]() .
.
Определение. Два вектора называются ортогональными, если их скалярное произведение равно нулю, то есть ![]() , причем
, причем ![]() .
.
Теорема 1. Всякая система ненулевых векторов, составленная из попарно ортогональных векторов, линейно независима.
Определение. Базис линейного пространства называется ортогональным, если его векторы попарно образуют ортогональную систему, и ортонормированным, если он ортогональный и каждый его вектор единичный.
Таким образом, если ![]() ортонормированный базис, то
ортонормированный базис, то 
Канонический базис ортонормирован. Заметим, что обратная матрица к матрице перехода от одного ортонормированного базиса к другому ортонормированному базису совпадает со своей транспонированной. Такие матрицы называются ортогональными. Примером ортонормированного базиса в ![]() является декартов базис
является декартов базис ![]() .
.
Пример 5. Вектор ![]() в базисе
в базисе ![]() ,
, ![]() ,
, ![]() имеет координаты
имеет координаты ![]() . Найти координаты вектора
. Найти координаты вектора ![]() в базисе
в базисе 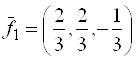 ,
, 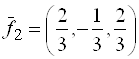 ,
,  .
.
Решение. Обратим внимание на то, что оба базиса ортонормированы. Мы уже знаем, что канонический базис ортонормирован. Базис ![]() также ортонормирован, так как
также ортонормирован, так как ![]() и
и ![]() .
.
Обозначим координаты вектора ![]() в базисе
в базисе ![]() через
через ![]() . Построим матрицу перехода от
. Построим матрицу перехода от ![]() к
к ![]() :
:  .
.
Эта матрица ортогональна, так как является матрицей перехода от одного ортонормированного базиса к другому ортонормированному базису. Поэтому: ![]() (
(![]() – транспонированная).
– транспонированная).
 .
.
Для самостоятельной работы.
1. Доказать, что каждая из двух систем векторов ![]() ,
, ![]() ,
, ![]() и
и ![]() ,
, ![]() ,
, ![]() является базисом и найти связь координат одного и того же вектора в этих двух базисах.
является базисом и найти связь координат одного и того же вектора в этих двух базисах.
Ответ: ![]()
![]()
![]()
2. Как изменится матрица перехода от одного базиса к другому, если:
А) поменять местами два вектора первого базиса?
Б) поменять местами два вектора второго базиса?
В) записать векторы обоих базисов в обратном порядке?
Ответ: а) поменяются местами две строки;
Б) поменяются местами два столбца;
В) произойдет транспонирование матрицы.
3. Относительно базиса ![]() ,
, ![]() ,
, ![]() даны четыре вектора
даны четыре вектора 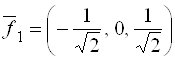 ,
, ![]() ,
,  ,
, ![]() .
.
Доказать, что ![]() образуют ортонормированный базис в
образуют ортонормированный базис в ![]() . Найти координаты вектора
. Найти координаты вектора ![]() в базисе
в базисе ![]() .
.
Ответ: ![]() .
.
| < Предыдущая | Следующая > |
|---|