4.3.3 Формулы перехода от одного базиса к другому

Очевидно, что в одном и том же пространстве можно выбрать множество базисов. Пусть в выбрано два базиса и .

Векторы базиса могут быть выражены через векторы базиса :

(4)

Матрица 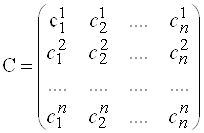называется матрицей перехода от базиса к базису . В ее столбцах записаны координаты векторов относительно базиса .

Соотношения (4) называются формулами перехода от базиса к базису . Их можно записать в матричной форме:

, отсюда .

Пусть вектор задан своими координатами относительно базиса – , а относительно базиса – . Тогда

и . (5)

Пример 4. Относительно базиса , , даны четыре вектора , , и . Векторы можно принять за базис в . Найти координаты вектора в базисе .

Решение. Матрица перехода от базиса к базису имеет вид . Обозначим координаты вектора в базисе через . Согласно формулам (5), имеем:

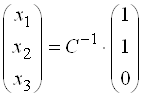. Находим : ;

; ; ;

; ; ;

; ; ;

.

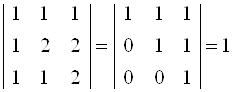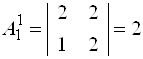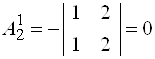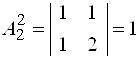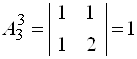Проверка: ;

;

или .

< Предыдущая		Следующая >