4.3.2 Базис и размерность линейных пространств. Координаты вектора

Понятие базиса линейного пространства тесно связано с понятием линейной зависимости векторов. Для векторов линейного пространства вводятся понятия линейной комбинации, линейной зависимости и линейной независимости системы векторов аналогично введенным в векторной алгебре и для столбцов (строк) матрицы. Справедливы также и теоремы о линейной зависимости.

Дадим критерий линейной зависимости и линейной независимости векторов в арифметическом пространстве.

Теорема 1. Векторы , , … , арифметического пространства линейно зависимы тогда и только тогда, когда ранг матрицы меньше числа векторов . Необходимым и достаточным условием их линейной независимости является равенство .

Из этой теоремы следует, что векторы

(1)

Линейно независимы.

Определение. Линейное пространство называется n-мерным, если в нем существует система из линейно независимых векторов, а любая система, составленная из векторов, линейно зависима. Обозначается .

Таким образом, размерность пространства – это максимальное число, содержащихся в нем линейно независимых векторов. Пространства, имеющие конечную размерность, называются конечномерными. Пространства, в которых можно найти сколько угодно линейно независимых векторов, называются бесконечномерными.

Определение. Любая совокупность из линейно независимых векторов -мерного линейного пространства называется базисом этого пространства.

Отметим, что базис пространства определяется неоднозначно, но все его базисы насчитывают одно и то же число векторов.

Система векторов (1) образует базис арифметического пространства, который называют каноническим базисом.

Следующая теорема демонстрирует фундаментальную роль базиса в представлении векторов наборами чисел (ключевая идея аналитической геометрии, восходящая к Декарту).

Теорема 2. Любой вектор из можно единственным образом представить в виде линейной комбинации базисных векторов.

Если векторы образуют базис пространства , а – любой вектор из , то на основании теоремы

. (2)

Правая часть (2) представляет собой линейную комбинацию векторов с коэффициентами .

Определение. Коэффициенты линейной комбинации, с помощью которой вектор выражается через базисные векторы, называются координатами относительно этого базиса.

Таким образом, числа в выражении (2) являются координатами вектора относительно базиса .

Координаты вектора относительно выбранного базиса определяются единственным образом.

Так же, как и в векторной алгебре справедлива теорема о том, что линейные операции над векторами сводятся к таким же операциям над их соответствующими координатами.

Итак, если в линейном пространстве выбран базис, то сложение векторов и умножение вектора на число выполняется так же, как и в арифметическом пространстве. При этом между векторами из и векторами из арифметического пространства можно установить взаимно-однозначное соответствие, сопоставив каждому вектору из вектор из арифметического пространства. Очевидно, что линейной комбинации векторов из соответствует точно такая же линейная комбинация соответствующих векторов арифметического пространства. Другими словами, произвольное линейное пространство изоморфно арифметическому пространству, откуда следует, что из всех -мерных линейных пространств достаточно изучить одно из них, например, арифметическое. В частности, теорему 1 можно сформулировать для любого линейного пространства :

Теорема 1. Векторы линейного пространства линейно зависимы тогда и только тогда, когда ранг матрицы, составленной из координат этих векторов относительно какого-нибудь базиса, меньше . Необходимым и достаточным условием их линейной независимости является равенство .

Заметим, что фундаментальная система решений системы линейных однородных уравнений является базисом пространства решений этой системы.

Пример 1. Доказать, что векторы , , пространства линейно зависимы. Найти коэффициенты линейной комбинации.

Решение. Докажем, что векторы линейно зависимы. Для этого найдем ранг матрицы :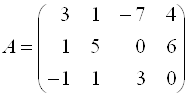

;

Первая и вторая строки одинаковы, поэтому одну из них можно вычеркнуть. Отсюда следует, что ранг матрицы равен 2, так как в матрице есть минор второго порядка 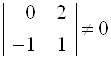. Ранг матрицы меньше числа векторов, следовательно векторы линейно зависимы. Это значит, что существуют числа , среди которых есть отличные от нуля, такие, что . Так как линейные операции над векторами сводятся к таким же операциям над их соответствующими координатами, то Можно найти из системы

.

Пунктиром выделен базисный минор. Свободное неизвестное . Находим общее решение системы:

;

– общее решение системы.

Базис пространства решений (фундаментальная система решений) состоит из одного вектора.

Если , то . Отсюда .

Пример 2. Относительно канонического базиса заданы четыре вектора: , , , . Образует ли система векторов базис линейного пространства ?

Решение. Составим матрицу из координат векторов и найдем ее ранг:

.

Ранг матрицы равен 4 и равен количеству векторов. Значит векторы линейно независимы, поэтому их можно принять за базис в пространстве .

Пример 3. Относительно канонического базиса , , пространства даны четыре вектора , , и . Доказать, что векторы можно принять за базис пространства и найти координаты вектора В этом базисе.

Решение. Составим матрицу из координат векторов . Докажем, что ранг этой матрицы равен 3 или, что то же самое, определитель, составленный из координат этих векторов, отличен от нуля.

.

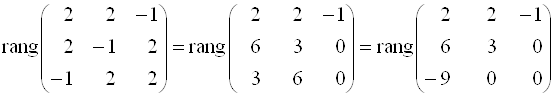Ранг матрицы равен 3 и равен числу векторов. Определитель этой матрицы равен . Значит векторы можно принять за базис. Как найти координаты вектора В этом базисе?

В базисе вектор имеет координаты , то есть его разложение по базису имеет вид . Нам же нужно получить разложение вектора по базису , то есть

, (3)

Где – координаты в базисе .

Так как векторы даны в базисе , то , , .

Подставим в (3) выражения через :

.

Так как координаты вектора относительно одного и того же базиса определяются единственным образом, то имеем:

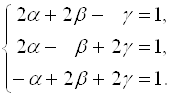
Эта система имеет единственное решение, так как

Ее определитель .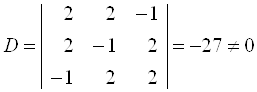

Замечание: здесь знак ~ означает, что если выписать системы с полученными матрицами, то они будут эквивалентными.

Отсюда:

.

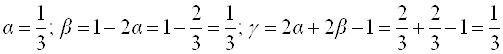Таким образом, . Подставляя эти значения в систему, в каждом уравнении получим тождество.

Относительно базиса вектор имеет координаты , то есть 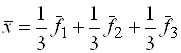. Обобщим результат этой задачи.

< Предыдущая		Следующая >