4.2 Системы линейных уравнений
Произвольная система линейных уравнений имеет вид
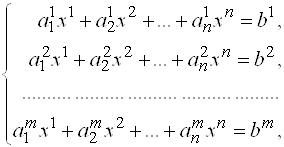 (1)
(1)
Где ![]() и
и ![]() – натуральные числа. Числа
– натуральные числа. Числа ![]() называются коэффициентами системы,
называются коэффициентами системы, ![]() – свободными членами и являются заданными,
– свободными членами и являются заданными, ![]() называются неизвестными и являются искомыми. Кратко систему можно записать в виде
называются неизвестными и являются искомыми. Кратко систему можно записать в виде ![]() .
.
Определение. Решением системы (1) называется всякая совокупность чисел ![]() , подстановка которых в систему (1) вместо соответствующих неизвестных обращает каждое уравнение системы в тождество.
, подстановка которых в систему (1) вместо соответствующих неизвестных обращает каждое уравнение системы в тождество.
Подчеркнем, что набор ![]() – одно решение системы (1), то есть
– одно решение системы (1), то есть ![]() .
.
Определение. Две системы называются эквивалентными, если решение первой является решением второй и наоборот.
Определение. Система, имеющая хотя бы одно решение, называется совместной. Система, не имеющая ни одного решения, называется несовместной.
Определение. Система, имеющая единственное решение, называется определенной, а имеющая более одного решения – неопределенной.
При решении систем линейных уравнений возникают следующие вопросы:
1) является ли система совместной;
2) если система совместна, то определенна или неопределенна;
3) если система определенна, то как найти ее единственное решение;
4) если система неопределенна, то как описать множество ее решений.
С системой линейных уравнений связаны две матрицы: матрица, составленная из коэффициентов при неизвестных  , которая называется основной, и матрица
, которая называется основной, и матрица 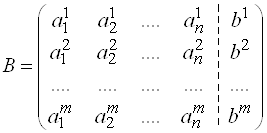 , получаемая добавлением к основной матрице столбца свободных членов и называемая расширенной матрицей системы (1).
, получаемая добавлением к основной матрице столбца свободных членов и называемая расширенной матрицей системы (1).
Критерий совместности системы (1) дает следующая теорема.
Теорема Кронекера-Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы равен рангу расширенной.
Если все свободные члены системы (1) равны нулю, то система называется однородной, в более общем случае, когда хотя бы один из свободных членов отличен от нуля – неоднородной.
Однородная система линейных уравнений всегда совместна, так как для нее ![]() (столбец, состоящий из нулей, вычеркивается при подсчете ранга матрицы).
(столбец, состоящий из нулей, вычеркивается при подсчете ранга матрицы).
Рассмотрение методов решения систем линейных уравнений начнем с частного вида систем, когда ![]() , то есть, когда число уравнений совпадает с числом неизвестных.
, то есть, когда число уравнений совпадает с числом неизвестных.
| < Предыдущая | Следующая > |
|---|