4.1.5 Линейная зависимость между столбцами матрицы. Понятие о ранге матрицы

Пусть даны две числовые матрицы, состоящие из одного столбца и . Операции сложения столбцов и умножения столбцов на число определяются следующим образом:

, .

Матрицу называют линейной комбинацией столбцов .

Определение. Совокупность столбцов называется линейно зависимой, если найдутся такие числа , среди которых хотя бы одно не равно нулю, что

(*)

(здесь 0 – нуль-столбец, т. е. столбец, все элементы которого равны нулю). Если равенство (*) возможно только в случае, когда все , то столбцы называются линейно независимыми. (Сравните с аналогичным определением для совокупности векторов).

Справедливы теоремы о линейной зависимости между столбцами, аналогичные соответствующим теоремам для векторов.

Определение. Пусть дана матрица размера . Выделим в этой матрице какие-либо строк и столбцов. На их пересечении получится квадратная матрица -го порядка. Ее определитель называется минором -го порядка матрицы .

(Не путайте понятия «минора данного элемента» и «минор -го порядка»).

Определение. Число называется рангом матрицы , если:

1) в матрице есть минор порядка , отличный от нуля;

2) все миноры порядка и выше, если они существуют, равны нулю.

Иначе, ранг матрицы – это наивысший порядок минора, отличного от нуля.

Обозначения: , , или .

Из определения следует, что – целое положительное число. Для нуль-матрицы считают ранг равным нулю.

Определение. Пусть дана матрица ранга . Любой минор матрицы, отличный от нуля и имеющий порядок , называется базисным, а строки и столбцы его составляющие – базисными строками и столбцами.

Согласно этому определению, матрица может иметь несколько базисных миноров.

Пример 14. Даны две матрицы , 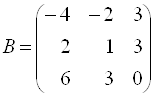и их миноры 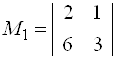, 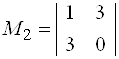. Какой из них можно принять в качестве базисного?

Решение. Минор , поэтому он не может быть базисным ни для одной из матриц. Минор и имеет порядок 2, значит его можно принять в качестве базисного матриц или / и при условии, что они имеют ранги, равные 2. Поскольку (как определитель с двумя пропорциональными столбцами), то и можно взять за базисный минор матрицы . Ранг матрицы равен 3, в силу того, что и, следовательно, порядок базисного минора этой матрицы должен равняться 3, то есть не является базисным для матрицы . Отметим, что у матрицы единственный базисный минор, равный определителю матрицы .

Теорема (о базисном миноре). Любая строка (столбец) матрицы является линейной комбинацией ее базисных строк (столбцов).

Следствия из теоремы.

1. Всякие столбцов (строк) матрицы ранга r линейно зависимы.

2. Если ранг матрицы меньше числа ее строк (столбцов), то ее строки (столбцы) линейно зависимы. Если равен числу ее строк (столбцов), то строки (столбцы) линейно независимы.

3. Определитель матрицы равен нулю тогда и только тогда, когда ее строки (столбцы) линейно зависимы.

4. Если к строке (столбцу) матрицы прибавить другую строку, (столбец) умноженную на любое число, отличное от нуля, то ранг матрицы не изменится.

5. Если в матрице зачеркнуть строку (столбец), являющуюся линейной комбинацией других строк (столбцов), то ранг матрицы не изменится.

6. Ранг матрицы равен максимальному числу ее линейно независимых строк (столбцов).

7. Максимальное число линейно независимых строк совпадает с максимальным числом линейно независимых столбцов.

Пример 15. Найти ранг матрицы

.

Решение. Исходя из определения ранга матрицы, будем искать минор наивысшего порядка, отличный от нуля. Сначала преобразуем матрицу к более простому виду. Для этого первую строку матрицы умножим на и прибавим ко второй, затем ее же умножим на и прибавим к третьей:

.

Поскольку вторая и третья строки пропорциональны, то одну из них можно вычеркнуть, что не изменит ранг. Получаем , так как в матрице есть минор второго порядка, отличный от нуля, а миноры более высокого порядка отсутствуют.

Пример 16. Найти ранг матрицы

.

Решение. Получим нули в первом столбце, оперируя первой строкой .

Третью строку вычеркиваем, поскольку она получается умножением второй строки на 2, а в последней строке отбросим общий множитель:

.

Для самостоятельного решения.

1. Найти ранг матрицы .

Ответ: .

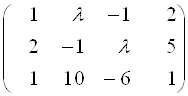2. При каких ранг матрицы Равен 2? равен 3?

Ответ: при ранг равен 2, при ранг равен 3.

3. Столбцы матрицы порядка связаны соотношением , где . Входят ли столбцы 1, 2, 3, 4 в базисный минор?

4. Дана матрица . Каков ее ранг?

5. Матрица порядка 3 составлена из трех ненулевых попарно неколлинеарных компланарных векторов. Укажите ранг матрицы.

6. Даны три матрицы:

Числа – максимально возможные порядки базисных миноров соответствующих матриц. Укажите наибольшее из этих чисел.

< Предыдущая		Следующая >