4.2.1 Решение систем линейных уравнений в случае

Система, в которой число неизвестных равно числу уравнений, называется квадратной; ее основная матрица также является квадратной. В случае система (1) тогда и только тогда является определенной, когда определитель основной матрицы отличен от нуля. Укажем способы решения таких систем.

I способ. Метод Крамера.

Если , то единственное решение системы находится по формулам

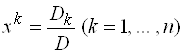, (2)

Где – определитель, получаемый из заменой -го столбца на столбец свободных членов.

Формулы (2) называют формулами Крамера.

II способ. Матричный метод.

Систему линейных уравнений

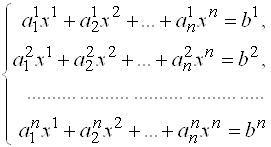
Можно записать в матричной форме

, (3)

Где , , ,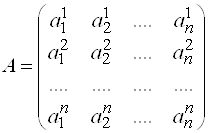

Или в виде

, (4)

Где , ,

.

Матричные уравнения вида (3) и (4) рассмотрены в пункте 4.1.4.

Пример 17. Доказать, что система 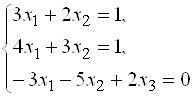имеет единственное решение и найти его двумя способами:

А) по формулам Крамера; б) матричным методом.

Решение:

А) найдем определитель основной матрицы:

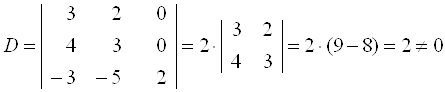, следовательно система имеет единственное решение.

,

,

По формулам Крамера находим , , .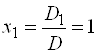

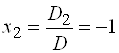Б) Запишем систему в матричной форме:

, откуда , где – обратная к основной матрице системы. .

; ; ;

; ; ;

; ; .

, ,

.

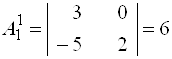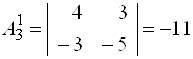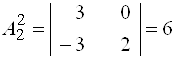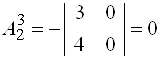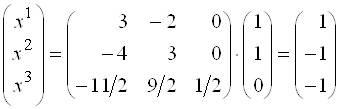III Метод Гаусса-Жордано (метод исключения неизвестных).

Суть этого метода разберем на примере.

Пример 18. Методом Гаусса решить систему

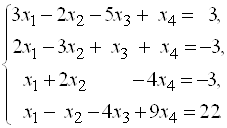
Заметим, что при работе с системой нет необходимости выписывать полностью ее уравнения, так как вся информация о системе содержится в ее расширенной матрице. Имея в виду возможную перестановку слагаемых, столбцы матрицы нумеруют согласно нумерации неизвестных.

Выпишем основную и расширенную матрицы и, оперируя только строками, приводим основную матрицу к треугольному виду:

Для удобства поменяем строки местами, чтобы в левом верхнем углу была единица.

Работаем первой строкой (сама она остается неизменной), для чего по очереди умножая ее на , , и складывая со 2, 3, 4 строками, получим нули в первом столбце:

Теперь, с целью получения единицы во второй строке, умножим третью строку на и прибавим ко второй:

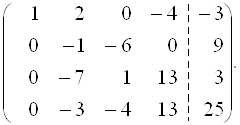
Умножим вторую строку на и сложим со второй, затем ее же умножим на и прибавим к последней строке:

Теперь последнюю строку умножим на и прибавим к предыдущей строке:

По этой матрице записываем систему, эквивалентную исходной:

Откуда находим: .

Для проверки достаточно подставить найденные значения неизвестных в каждое уравнение системы и убедиться, что все они обратятся в тождества.

< Предыдущая		Следующая >