4.2.3 Системы линейных однородных уравнений

Рассмотрим систему вида

, (1)

Где или .

Однородная система линейных уравнений (1) всегда совместна, так как . Она заведомо имеет решение, состоящее из нулей , которое называется тривиальным.

В каких случаях существует нетривиальное решение?

Теорема. Для того чтобы система (1) имела нетривиальные решения, необходимо и достаточно, чтобы ранг ее матрицы был меньше числа неизвестных.

Действительно, в этом случае есть свободные неизвестные, которым можно придавать любые, в том числе и ненулевые, значения.

Выделим частный случай систем (1), когда .

Теорема. Система (1) в случае имеет нетривиальное решение тогда и только тогда, когда определитель этой системы равен нулю.

Системы линейных однородных уравнений обладают важным свойством, которое сформулируем в виде теоремы.

Теорема. Любая линейная комбинация решений системы (1) также является решением этой системы.

Возникает вопрос, можно ли подобрать такую совокупность решений системы (1), чтобы любое решение системы можно было бы найти как линейную комбинацию этих решений? Такая совокупность решений существует и носит название фундаментальной.

Определение. Совокупность решений системы линейных однородных уравнений (1) называется фундаментальной системой решений, если эта совокупность состоит из линейно независимых решений и любое решение системы (1) является линейной комбинацией этих решений.

Теорема. Если ранг матрицы системы (1) меньше числа n неизвестных, то существует фундаментальная система решений, состоящая из решений.

Пример 22. Найти общее решение и какую-нибудь фундаментальную систему решений для системы

Решение. Алгоритм решения такой же, как и для систем линейных неоднородных уравнений.

Оперируя только со строками, находим ранг матрицы, базисный минор; объявляем зависимые и свободные неизвестные и находим общее решение.

Первая и вторая строки пропорциональны, одну из них вычеркнем:

.

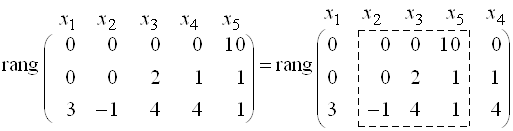Зависимые переменные – , свободные – . Из первого уравнения находим , тогда

; .

Общее решение имеет вид:

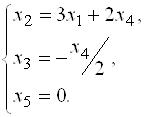
Находим фундаментальную систему решений, которая состоит из решений. В нашем случае , следовательно, фундаментальная система решений состоит из двух решений, причем эти решения должны быть линейно независимыми. Чтобы строки были линейно независимыми, необходимо и достаточно, чтобы ранг матрицы, составленной из элементов строк, был равен количеству строк, то есть 2. Достаточно придать свободным неизвестным и значения из строк определителя второго порядка, отличного от нуля, и подсчитать . Простейшим определителем, отличным от нуля, является .

Таким образом, первое решение: , второе – .

Эти два решения составляют фундаментальную систему решений. Заметим, что фундаментальная система не единственна (определителей, отличных от нуля, можно составить сколько угодно).

Пример 22. Найти общее решение и фундаментальную систему решений системы

Решение.

,

Отсюда следует, что ранг матрицы равен 3 и равен числу неизвестных. Значит, система не имеет свободных неизвестных, а поэтому имеет единственное решение – тривиальное.

Для самостоятельного решения.

1. Доказать, что система 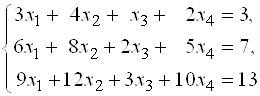совместна.

Найти ее общее и частное решения, приняв в качестве свободных неизвестных и полагая .

Ответ: .

2. Образуют ли строки каждой из матриц и , где 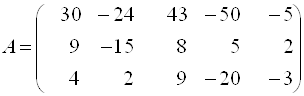, , 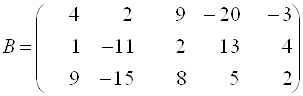фундаментальную систему решений для системы

Ответ: строки матрицы не образуют фундаментальную систему решений, строки матрицы образуют.

3. Три прямые , , образуют треугольник. Охарактеризовать систему трех уравнений с точки зрения совместности и ранга матрицы коэффициентов.

Ответ выбрать из списка: 1) система совместна, ; 2) система несовместна, ; 3) совместна любая пара уравнений, .

< Предыдущая		Следующая >