3.2 Плоскость
Уравнение плоскости, проходящей через точку ![]() перпендикулярно вектору
перпендикулярно вектору ![]() , имеет вид
, имеет вид
![]() , (12)
, (12)
Или
![]() , (13)
, (13)
Где ![]() . Уравнение (13) называется общим уравнением плоскости. Вывод этого уравнения полностью повторяет вывод общего уравнения прямой на плоскости.
. Уравнение (13) называется общим уравнением плоскости. Вывод этого уравнения полностью повторяет вывод общего уравнения прямой на плоскости.
Еще раз подчеркнем геометрический смысл каждой буквы, входящей в уравнения (12) и (13): ![]() – координаты текущей точки плоскости,
– координаты текущей точки плоскости, ![]() – координаты фиксированной точки плоскости,
– координаты фиксированной точки плоскости, ![]() – координаты любого вектора перпендикулярного плоскости, называемого нормалью плоскости.
– координаты любого вектора перпендикулярного плоскости, называемого нормалью плоскости.
Если коэффициенты уравнения (13) не равны нулю, то его можно привести к виду  , где
, где ![]() – отрезки, отсекаемые плоскостью на осях координат, поэтому это уравнение называют уравнением плоскости в отрезках.
– отрезки, отсекаемые плоскостью на осях координат, поэтому это уравнение называют уравнением плоскости в отрезках.
Всякое уравнение первой степени в пространстве определяет плоскость.
Расстояние от точки ![]() до плоскости, заданной в виде (13), находится по формуле
до плоскости, заданной в виде (13), находится по формуле
 . (14)
. (14)
Двугранный угол между плоскостями ![]() и
и ![]() совпадает с углом между их нормалями и вычисляется по формуле
совпадает с углом между их нормалями и вычисляется по формуле
 . (15)
. (15)
Если плоскости параллельны, то ![]() , следовательно, их координаты пропорциональны
, следовательно, их координаты пропорциональны 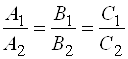 – условие параллельности плоскостей.
– условие параллельности плоскостей.
Условие ортогональности плоскостей можно записать в виде ![]() или в координатной форме
или в координатной форме ![]() .
.
Пример 1. Можно ли однозначно ответить на вопрос: «Прямую или плоскость определяет уравнение ![]() ?»
?»
*** Однозначного ответа на поставленный вопрос дать нельзя, так как если это уравнение рассматривать на плоскости, то оно описывает прямую, если же в пространстве, то оно задает плоскость, одна из координат нормали которой равна нулю.
 Пример 2. Составить уравнение плоскости, проходящей через точку
Пример 2. Составить уравнение плоскости, проходящей через точку ![]() параллельно плоскости
параллельно плоскости ![]() .
.
Решение. У параллельных плоскостей общая нормаль ![]() , тогда по формуле (12) получим
, тогда по формуле (12) получим ![]() или
или ![]() .
.
Укажем два способа нахождения уравнения плоскости:
I. Воспользоваться готовым уравнением плоскости (12) или (13) и тогда дело сведется к нахождению любой фиксированной точки плоскости и любого вектора, перпендикулярного искомой плоскости.
II. Решать задачу средствами векторной алгебры, не используя уравнений (12), (13).
Проиллюстрируем сказанное примером.
Пример 3. Написать уравнение плоскости, проходящей через точку ![]() параллельно векторам
параллельно векторам ![]() и
и ![]() .
.
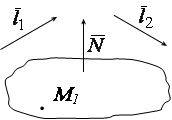 Первый способ. Чертеж рекомендуем делать обязательно. Фиксированная точка дана по условию. Осталось найти нормаль
Первый способ. Чертеж рекомендуем делать обязательно. Фиксированная точка дана по условию. Осталось найти нормаль ![]() . Вектор
. Вектор ![]() и
и ![]() . Подобная ситуация – когда один вектор ортогонален одновременно двум другим векторам, встречалась в векторной алгебре при определении векторного произведения векторов. Напомним: если
. Подобная ситуация – когда один вектор ортогонален одновременно двум другим векторам, встречалась в векторной алгебре при определении векторного произведения векторов. Напомним: если ![]() , то: 1)
, то: 1) ![]() ,
,![]() ; 2)
; 2) ![]() – правая тройка; 3)
– правая тройка; 3) 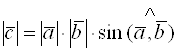 . Второе условие говорит об ориентации
. Второе условие говорит об ориентации ![]() , а третье – о его длине. Поскольку ни длина, ни ориентация
, а третье – о его длине. Поскольку ни длина, ни ориентация ![]() не играют никакой роли, а первое условие выполнено, то нормаль можно найти как векторное произведение
не играют никакой роли, а первое условие выполнено, то нормаль можно найти как векторное произведение ![]() и
и ![]() :
:
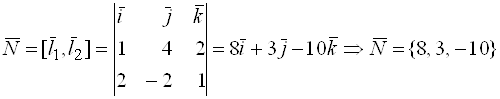 .
.
Подставляя координаты точки ![]() и
и ![]() в уравнение (12), получим
в уравнение (12), получим ![]() , откуда
, откуда ![]() .
.
Проверка. Так как ![]() и
и ![]() , то
, то ![]() и
и ![]() . Действительно:
. Действительно: ![]() и
и ![]() . Точка
. Точка ![]() должна принадлежать плоскости:
должна принадлежать плоскости: ![]() . Задача решена верно.
. Задача решена верно.
 Второй способ. На чертеже не изображена нормаль искомой плоскости, так как мы будем решать задачу, не используя уравнения плоскости, а значит ничего не зная о ее нормали.
Второй способ. На чертеже не изображена нормаль искомой плоскости, так как мы будем решать задачу, не используя уравнения плоскости, а значит ничего не зная о ее нормали.
Уравнение какого бы то ни было геометрического образа невозможно составить без текущей точки. Возьмем на плоскости текущую точку ![]() и соединим ее с точкой
и соединим ее с точкой ![]() . Получим вектор
. Получим вектор ![]() .
.
Векторы ![]() ,
, ![]() и
и ![]() компланарны, следовательно
компланарны, следовательно ![]() . Это и будет уравнение искомой плоскости в векторной форме, так как ему удовлетворяет любая точка этой плоскости и не удовлетворяет никакая другая точка (если взять точку
. Это и будет уравнение искомой плоскости в векторной форме, так как ему удовлетворяет любая точка этой плоскости и не удовлетворяет никакая другая точка (если взять точку ![]() , лежащую выше или ниже плоскости, то
, лежащую выше или ниже плоскости, то ![]() не будет лежать в плоскости и
не будет лежать в плоскости и ![]() ,
, ![]() ,
, ![]() не будут компланарными, а значит их смешанное произведение не равно нулю).
не будут компланарными, а значит их смешанное произведение не равно нулю).
В координатной форме уравнение плоскости будет иметь вид  , или, раскрывая определитель,
, или, раскрывая определитель, ![]() .
.
Пример 4. Написать общее уравнение плоскости, проходящей через точку ![]() параллельно оси
параллельно оси ![]() и перпендикулярно к плоскости
и перпендикулярно к плоскости ![]() .
.
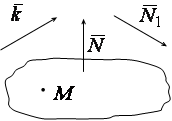 Решение. Выберем на оси
Решение. Выберем на оси ![]() любой вектор, например
любой вектор, например ![]() . Сделаем чертеж. Рекомендуем на чертеже изобразить только искомую плоскость, а положение плоскости
. Сделаем чертеж. Рекомендуем на чертеже изобразить только искомую плоскость, а положение плоскости ![]() обозначить ее нормалью
обозначить ее нормалью ![]() (так как эти плоскости перпендикулярны, то
(так как эти плоскости перпендикулярны, то ![]() параллельна искомой). Так как
параллельна искомой). Так как ![]() и
и ![]() , то
, то
 .
.
Подставляя координаты точки ![]() и вектора
и вектора ![]() в уравнение (12), получим искомое уравнение
в уравнение (12), получим искомое уравнение ![]() .
.
Пример 5. Даны вершины треугольника ![]() ,
, ![]() ,
, ![]() . Через сторону
. Через сторону ![]() провести плоскость перпендикулярно плоскости треугольника.
провести плоскость перпендикулярно плоскости треугольника.
 Решение. Составим уравнение плоскости (плоскости треугольника), проходящей через три данные точки. Найдем
Решение. Составим уравнение плоскости (плоскости треугольника), проходящей через три данные точки. Найдем ![]() ,
, ![]() ,
,
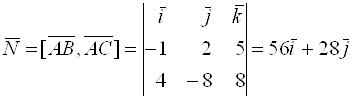 ,
,
![]() .
.
 Уравнение плоскости треугольника:
Уравнение плоскости треугольника: ![]() . Теперь задача свелась к нахождению уравнения плоскости, проходящей через
. Теперь задача свелась к нахождению уравнения плоскости, проходящей через ![]() перпендикулярно плоскости
перпендикулярно плоскости ![]() .
.
Так как ![]() и
и ![]() , то
, то
 .
.
Возьмем ![]() , тогда получим из (12)
, тогда получим из (12) ![]() ,
, ![]() .
.
Пример 6. Через точки ![]() и
и ![]() провести плоскость, образующую угол
провести плоскость, образующую угол ![]() с плоскостью
с плоскостью ![]() .
.
Решение. Будем искать уравнение плоскости в виде ![]() , где
, где ![]() . Так как
. Так как ![]() , то
, то ![]() или в координатах:
или в координатах: ![]() . По формуле (15):
. По формуле (15): 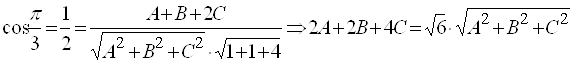 . Для нахождения трех неизвестных
. Для нахождения трех неизвестных ![]() получаем систему
получаем систему

Уменьшим число неизвестных, разделив обе части на ![]() :
:
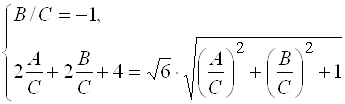 , откуда
, откуда 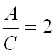 .
.
Получили ![]() . В качестве нормали возьмем
. В качестве нормали возьмем ![]() . Уравнение плоскости:
. Уравнение плоскости: ![]() или
или ![]() .
.
Для самостоятельного решения.
1. При каких значениях ![]() и
и ![]() плоскости
плоскости ![]() и
и ![]() будут параллельны?
будут параллельны?
Ответ: ![]() ,
, ![]() .
.
2. Определить двугранные углы, образованные пересечением плоскостей ![]() и
и ![]() .
.
Ответ: ![]() и
и ![]() .
.
3. Составить уравнение плоскости, отсекающей на оси ![]() отрезок
отрезок ![]() и перпендикулярной вектору
и перпендикулярной вектору ![]() .
.
Ответ: ![]() .
.
4. Найти уравнение плоскости, проходящей через ось ![]() и точку
и точку ![]() .
.
Ответ: ![]() .
.
5. Написать уравнение плоскости, проходящей через точку ![]() перпендикулярно плоскостям
перпендикулярно плоскостям ![]() ,
, ![]() .
.
Ответ: ![]() .
.
6. Две грани куба расположены на плоскостях ![]() ,
, ![]() . Найти его объем.
. Найти его объем.
Ответ: ![]() .
.
7. Составить уравнение плоскости, параллельной плоскости ![]() и отстоящей от точки
и отстоящей от точки ![]() на расстоянии
на расстоянии ![]() .
.
Ответ: ![]() ,
, ![]() .
.
8. Найти уравнение плоскости, проходящей через точки ![]() и
и ![]() и перпендикулярной к плоскости
и перпендикулярной к плоскости ![]() .
.
Ответ: ![]() .
.
9. На оси ![]() найти точку, равноудаленную от точки
найти точку, равноудаленную от точки ![]() и от плоскости
и от плоскости ![]() .
.
Ответ: ![]() .
.
10. Найти высоту пирамиды ![]() , опущенную из вершины
, опущенную из вершины ![]() на грань
на грань ![]() , если
, если ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Ответ: ![]() .
.
| < Предыдущая | Следующая > |
|---|