3.3 Прямая в пространстве
Перечислим виды уравнений прямой в пространстве.
1. Прямую в пространстве можно задать как линию пересечения двух плоскостей, если нормали у них не параллельны:
 – общее уравнение.
– общее уравнение.
2. 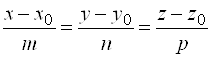 – канонические уравнения.
– канонические уравнения.
3.  – параметрические уравнения.
– параметрические уравнения.
Геометрический смысл букв, входящих в канонические и параметрические уравнения: ![]() – координаты текущей точки прямой,
– координаты текущей точки прямой, ![]() – координаты фиксированной точки прямой,
– координаты фиксированной точки прямой, ![]() – координаты направляющего вектора прямой.
– координаты направляющего вектора прямой.
Заметим, что в каждой точке пространственной прямой можно провести бесчисленное множество векторов, перпендикулярных к ней, не параллельных между собой. Поэтому задание нормали к прямой не определяет ее положения в пространстве. Чтобы составить канонические и параметрические уравнения прямой в пространстве, нужна фиксированная точка прямой и ее направляющий вектор.
Расстояние ![]() от точки
от точки ![]() до прямой
до прямой ![]() находится по формуле
находится по формуле
 , (16)
, (16)
Где ![]() – радиус-вектор точки
– радиус-вектор точки ![]() ,
, ![]() – радиус-вектор фиксированной точки прямой и
– радиус-вектор фиксированной точки прямой и ![]() – ее направляющий вектор.
– ее направляющий вектор.
Расстояние между двумя прямыми ![]() и
и ![]() , (
, (![]() не параллелен
не параллелен ![]() ) вычисляется по формуле
) вычисляется по формуле
 . (17)
. (17)
Условие пересечения прямых: ![]() . Если прямые скрещиваются, то
. Если прямые скрещиваются, то ![]() .
.
Чтобы перейти от общего уравнения к каноническим или параметрическим, надо найти фиксированную точку и направляющий вектор. Так как прямая задана как линия пересечения двух плоскостей, то все точки прямой принадлежат обеим плоскостям. Получаем два уравнения на три неизвестные. Одну из координат, например ![]() , полагаем равной любому числу (проще всего нулю) и, решая систему двух уравнений с двумя неизвестными, находим остальные две координаты.
, полагаем равной любому числу (проще всего нулю) и, решая систему двух уравнений с двумя неизвестными, находим остальные две координаты.
Если система окажется несовместной при выбранном ![]() (на прямой нет точки с такой аппликатой), то либо полагаем
(на прямой нет точки с такой аппликатой), то либо полагаем ![]() равному другому числу, либо полагаем
равному другому числу, либо полагаем ![]() или
или ![]() .
.
Направляющий вектор ![]() находим как векторное произведение
находим как векторное произведение ![]() и
и ![]() , так как
, так как ![]() и
и ![]() .
.
Пример 1. Написать канонические и параметрические уравнения прямой 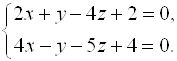
Решение. Положим ![]() , тогда получим
, тогда получим 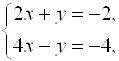 откуда находим
откуда находим ![]() ,
, ![]() . Фиксированная точка
. Фиксированная точка ![]() .
. ![]() ,
, ![]() ,
,  ,
, ![]() . Канонические уравнения:
. Канонические уравнения: 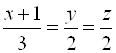 . Обозначая
. Обозначая 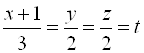 , получим параметрические уравнения:
, получим параметрические уравнения: ![]() ,
, ![]() ,
, ![]() .
.
Пример 2. Найти уравнение прямой, проходящей через точки ![]() и
и ![]() .
.
![]() Решение. В качестве фиксированной точки прямой можно взять любую из точек
Решение. В качестве фиксированной точки прямой можно взять любую из точек ![]() и
и ![]() . Направляющим вектором служит любой вектор, параллельный прямой (в частности, расположенный на самой прямой), поэтому
. Направляющим вектором служит любой вектор, параллельный прямой (в частности, расположенный на самой прямой), поэтому ![]() . Запишем уравнения
. Запишем уравнения 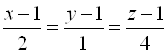 .
.
Пример 3. Вычислить расстояние от точки ![]() до прямой
до прямой 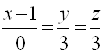 . Часто вызывает недоумение число нуль, стоящее в знаменателе (одна из координат направляющего вектора равна нулю). В этом случае полагают равным нулю соответствующий числитель, в данном случае
. Часто вызывает недоумение число нуль, стоящее в знаменателе (одна из координат направляющего вектора равна нулю). В этом случае полагают равным нулю соответствующий числитель, в данном случае ![]() – уравнение одной из плоскостей.
– уравнение одной из плоскостей.
Решение. Из уравнения прямой берем фиксированную точку ![]() и
и ![]() . Воспользуемся формулой
. Воспользуемся формулой  , где
, где ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.  .
. 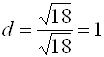 .
.
Пример 4. Указать значения ![]() , при которых прямые
, при которых прямые 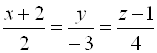 и
и  пересекаются.
пересекаются.
Решение. Из уравнений прямых находим ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Условие пересечения прямых
. Условие пересечения прямых ![]() запишем в координатной форме
запишем в координатной форме  , откуда
, откуда ![]() .
.
 Пример 5. Проверить, лежат ли прямые
Пример 5. Проверить, лежат ли прямые 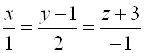 и
и 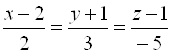 в одной плоскости.
в одной плоскости.
Решение. Из уравнения прямых находим ![]() ,
, ![]() ,
, ![]() ,
, ![]() , тогда
, тогда ![]() . Если прямые лежат в одной плоскости, то векторы
. Если прямые лежат в одной плоскости, то векторы ![]() компланарны, значит
компланарны, значит ![]() . Для проверки этого условия запишем его в координатной форме:
. Для проверки этого условия запишем его в координатной форме:
 , следовательно прямые не лежат в одной плоскости, т. е. скрещиваются.
, следовательно прямые не лежат в одной плоскости, т. е. скрещиваются.
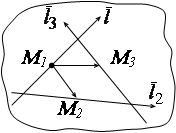 Пример 6. Составить уравнение прямой, которая проходит через точку
Пример 6. Составить уравнение прямой, которая проходит через точку ![]() и пересекает две прямые
и пересекает две прямые  и
и 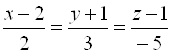 .
.
Решение. Из условия находим ![]() ,
, ![]() ,
, ![]() ,
, ![]() , тогда
, тогда ![]() ,
, ![]() .
.
Обозначим ![]() – направляющий вектор искомой прямой. Будем искать уравнение в виде
– направляющий вектор искомой прямой. Будем искать уравнение в виде 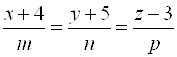 . Запишем условие пересечения двух прямых:
. Запишем условие пересечения двух прямых:  и
и  , откуда для нахождения
, откуда для нахождения ![]() получаем систему
получаем систему 
Так как число уравнений меньше числа неизвестных, то разделим уравнения, например, на ![]() :
: 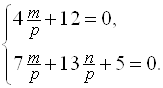 Решая эту систему относительно неизвестных
Решая эту систему относительно неизвестных ![]() и
и ![]() , найдем
, найдем 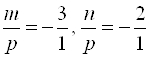 , или
, или ![]() .
.
Итак, ![]() . Канонические уравнения искомой прямой:
. Канонические уравнения искомой прямой:  .
.
Пример 7. Найти точку пересечения прямой  с плоскостью
с плоскостью ![]() .
.
Решение. Можно было бы от канонических уравнений прямой перейти к общему:  или
или 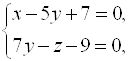 а затем найти точку пересечения трех плоскостей. Рациональней другой путь. Перейдем к параметрическим уравнениям прямой:
а затем найти точку пересечения трех плоскостей. Рациональней другой путь. Перейдем к параметрическим уравнениям прямой: ![]() ,
, ![]() ,
, ![]() . Подставим эти выражения для
. Подставим эти выражения для ![]() в уравнение плоскости:
в уравнение плоскости: ![]() , откуда
, откуда ![]() . Тогда
. Тогда ![]() ,
, ![]() ,
, ![]() .
.
Для самостоятельного решения.
1. Найти уравнение прямой, проходящей через точку ![]() параллельно прямой
параллельно прямой  .
.
Ответ:  .
.
2. Написать параметрические уравнения прямой 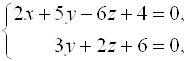 взяв в качестве фиксированной точки
взяв в качестве фиксированной точки ![]() .
.
Ответ: ![]() .
.
3. Найти расстояние между прямыми  и
и  .
.
Ответ: 3.
4. Найти угол между прямыми ![]() и
и 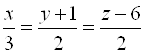 .
.
Ответ: ![]() .
.
5. Найти проекцию начала координат на прямую  .
.
Ответ: ![]() .
.
6. Найти уравнение перпендикуляра, опущенного из точки ![]() на прямую
на прямую 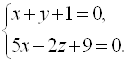 В ответе укажите координаты направляющего вектора.
В ответе укажите координаты направляющего вектора.
Ответ: ![]() .
.
7. Составить уравнение проекции прямой 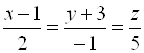 на плоскость
на плоскость ![]() . В ответе укажите координаты направляющего вектора.
. В ответе укажите координаты направляющего вектора.
Ответ: ![]() .
.
8. Прямая пересекает прямую 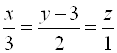 , оси
, оси ![]() и
и ![]() и параллельна плоскости
и параллельна плоскости ![]() . Найти длину отрезка искомой прямой между точками пересечения ее с осями координат.
. Найти длину отрезка искомой прямой между точками пересечения ее с осями координат.
Ответ: 5.
9. Выяснить взаимное расположение прямой  и плоскости
и плоскости ![]() . Если они не параллельны, найти их точку пересечения.
. Если они не параллельны, найти их точку пересечения.
Ответ: ![]() .
.
10. Найти точку ![]() , симметричную точке
, симметричную точке ![]() относительно прямой, проходящей через точки
относительно прямой, проходящей через точки ![]() и
и ![]() .
.
Ответ: ![]() .
.
| < Предыдущая | Следующая > |
|---|