3.1 Прямая на плоскости
Составим уравнение прямой, проходящей через заданную точку ![]() перпендикулярно ненулевому вектору
перпендикулярно ненулевому вектору ![]() .
.
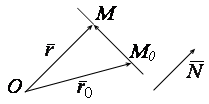 Пусть
Пусть ![]() – начало декартовой системы координат,
– начало декартовой системы координат, ![]() – переменная (текущая) точка искомой прямой,
– переменная (текущая) точка искомой прямой, ![]() – радиус-векторы точек
– радиус-векторы точек ![]() и
и ![]() соответственно.
соответственно.
Вектор ![]() лежит на прямой, следовательно,
лежит на прямой, следовательно, ![]() . Необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения. Так как
. Необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения. Так как ![]() , то получаем
, то получаем
![]() (1)
(1)
– уравнение прямой в векторной форме.
Возникает вопрос: почему условие ортогональности векторов в то же время назвали уравнением прямой? Ответ следует из определения 1: потому, что этому уравнению удовлетворяет любая точка, лежащая на прямой, и не удовлетворяет никакая другая, так как если точка ![]() не лежит на искомой прямой, то
не лежит на искомой прямой, то ![]() не будет перпендикулярен
не будет перпендикулярен ![]() , следовательно, условие (1) не выполняется.
, следовательно, условие (1) не выполняется.
Уравнение (1) в координатной форме примет вид:
![]() , (2)
, (2)
Или, обозначая ![]() :
:
![]() (3)
(3)
– общее уравнение прямой.
Для успешного применения формул (2) и (3) необходимо знать геометрический смысл каждой буквы, входящей в уравнения: ![]() – координаты фиксированной точки прямой,
– координаты фиксированной точки прямой, ![]() – координаты текущей точки прямой,
– координаты текущей точки прямой, ![]() – координаты вектора нормали к прямой.
– координаты вектора нормали к прямой.
Аналогично, решая задачу о нахождении уравнения прямой, проходящей через данную точку ![]() параллельно вектору
параллельно вектору ![]() , придем к уравнению
, придем к уравнению
![]() , (4)
, (4)
Которое называется параметрическим уравнением прямой в векторной форме. Здесь ![]() – переменная величина, называемая параметром. Любой вектор, параллельный прямой, называется направляющим вектором прямой. В качестве направляющего вектора
– переменная величина, называемая параметром. Любой вектор, параллельный прямой, называется направляющим вектором прямой. В качестве направляющего вектора ![]() , в частности, можно взять любой вектор, лежащий на прямой. Уравнение (4) можно записать в координатной форме:
, в частности, можно взять любой вектор, лежащий на прямой. Уравнение (4) можно записать в координатной форме:
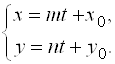 (5)
(5)
Исключая из уравнений (4) параметр ![]() , получим:
, получим:
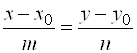 . (6)
. (6)
Уравнение (6) называют каноническим уравнением прямой. В частности, если прямая проходит через точки ![]() и
и ![]() , то в качестве
, то в качестве ![]() можно взять вектор
можно взять вектор ![]() и уравнение (6) записать в виде
и уравнение (6) записать в виде  .
.
В формулах (5) и (6) ![]() и
и ![]() – координаты направляющего вектора прямой, а смысл букв
– координаты направляющего вектора прямой, а смысл букв ![]() – тот же, что и в общем уравнении.
– тот же, что и в общем уравнении.
Обозначая ![]() , уравнение (3) перепишем в виде
, уравнение (3) перепишем в виде
![]() (7)
(7)
– уравнение прямой с угловым коэффициентом.
Уравнению (7) можно придать другой вид:
![]() , (8)
, (8)
Где ![]() – фиксированная точка прямой.
– фиксированная точка прямой.
От уравнения (8) можно перейти к уравнению (7), если обозначить ![]() . Величина
. Величина ![]() равна тангенсу угла наклона прямой к оси
равна тангенсу угла наклона прямой к оси ![]() ,
, ![]() – длина отрезка, отсекаемого прямой на оси
– длина отрезка, отсекаемого прямой на оси ![]() .
.
Заметим, что всякое уравнение первой степени на плоскости определяет прямую.
Расстояние от точки ![]() до прямой
до прямой ![]() находится по формуле:
находится по формуле:
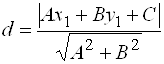 . (9)
. (9)
Угол между прямыми ![]() и
и ![]() можно найти по формуле:
можно найти по формуле:
 , (10)
, (10)
А если прямые заданы в виде ![]() , то по формуле
, то по формуле
 . (11)
. (11)
Общие рекомендации. Прежде всего, обратите внимание на геометрический смысл каждой буквы, входящей в уравнения прямой различного вида. В этом – ключ к решению задач на составление уравнения прямой. Каким бы ни было условие задачи, в конце концов, дело сведется к нахождению прямой, проходящей через фиксированную (заданную) точку, и при этом либо:
А) параллельно прямой;
б) перпендикулярно прямой;
в) под углом к другой прямой.
Проанализируйте, не решая, условия следующих задач:
1. Составить уравнение прямой, проходящей через точку ![]() и при этом:
и при этом:
А) параллельно прямой ![]() ;
;
Б) перпендикулярно прямой ![]() .
.
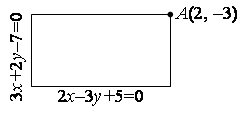 2. Даны уравнения двух сторон прямоугольника:
2. Даны уравнения двух сторон прямоугольника:
![]() ,
, ![]()
И одна из его вершин ![]() . Составить уравнения двух других сторон прямоугольника. Попутно разберитесь, почему на чертеже именно так выбраны прямые и точка.
. Составить уравнения двух других сторон прямоугольника. Попутно разберитесь, почему на чертеже именно так выбраны прямые и точка.
3. Составить уравнения прямых, проходящих через вершины треугольника ![]() параллельно противоположным сторонам.
параллельно противоположным сторонам.
4. Даны уравнения двух сторон прямоугольника ![]() ,
, ![]() и уравнение одной из его диагоналей
и уравнение одной из его диагоналей ![]() . Найти вершины прямоугольника.
. Найти вершины прямоугольника.
У этих задач разное содержание, но решение любой из них сведется к нахождению либо параллельной, либо перпендикулярной данной (известной) прямой. Поэтому надо направить усилия на отыскание либо нормали, либо направляющего вектора искомой прямой и в зависимости от того, что из них удается найти, выбрать форму (вид) уравнения – для общего уравнения нужна конкретная точка и нормаль, для канонического и параметрического уравнений нужна точка и направляющий вектор.
Заметим, что нормаль ![]() и направляющий вектор
и направляющий вектор ![]() одной и той же прямой перпендикулярны, значит
одной и той же прямой перпендикулярны, значит ![]() . Поэтому, зная координаты
. Поэтому, зная координаты ![]() , можно найти координаты
, можно найти координаты ![]() и наоборот.
и наоборот.
Решим первую из сформулированных выше задач.
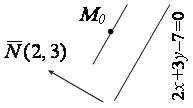 А) Из чертежа видно, что у двух прямых (заданной и искомой) общая нормаль, следовательно, можно написать общее уравнение искомой прямой:
А) Из чертежа видно, что у двух прямых (заданной и искомой) общая нормаль, следовательно, можно написать общее уравнение искомой прямой: ![]() или
или ![]() .
.
 Б) Как видим, нормаль к заданной прямой является направляющим вектором искомой прямой, поэтому можно написать каноническое уравнение искомой прямой:
Б) Как видим, нормаль к заданной прямой является направляющим вектором искомой прямой, поэтому можно написать каноническое уравнение искомой прямой: 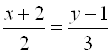 или
или ![]() .
.
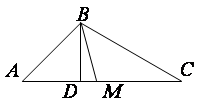 Пример 1. Треугольник задан координатами своих вершин
Пример 1. Треугольник задан координатами своих вершин ![]() ,
, ![]() ,
, ![]() . Написать:
. Написать:
А) уравнение стороны ![]() ;
;
Б) уравнение медианы ![]() ;
;
В) уравнение высоты ![]() ;
;
Г) уравнение биссектрисы внутреннего угла при вершине ![]() .
.
Решение. а) Найдем координаты вектора ![]() , который можно взять в качестве направляющего вектора, а в качестве фиксированной точки выберем, например, точку
, который можно взять в качестве направляющего вектора, а в качестве фиксированной точки выберем, например, точку ![]() . Так как по определению направляющий вектор – любой вектор, параллельный прямой, то, сокращая координаты вектора
. Так как по определению направляющий вектор – любой вектор, параллельный прямой, то, сокращая координаты вектора ![]() на
на ![]() , возьмем в качестве направляющего вектор
, возьмем в качестве направляющего вектор ![]() и запишем каноническое уравнение прямой
и запишем каноническое уравнение прямой ![]() :
:  , от которого легко перейти к параметрическим
, от которого легко перейти к параметрическим 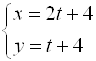 , или к общему
, или к общему ![]() .
.
Б) Точка ![]() – середина отрезка
– середина отрезка ![]() , следовательно ее координаты
, следовательно ее координаты ![]() , а вектор
, а вектор ![]() служит направляющим вектором. Уравнение медианы
служит направляющим вектором. Уравнение медианы ![]() в канонической форме:
в канонической форме: 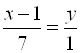 или
или ![]() .
.
В) Так как прямые ![]() и
и ![]() перпендикулярны, то в качестве нормали к
перпендикулярны, то в качестве нормали к ![]() можно взять
можно взять ![]() или любой вектор, ему параллельный, в частности
или любой вектор, ему параллельный, в частности ![]() . По формуле (2) получим:
. По формуле (2) получим: ![]() или
или ![]() .
.
 Г) Известно, что диагонали ромба делят углы пополам. Найдем орты
Г) Известно, что диагонали ромба делят углы пополам. Найдем орты ![]() и
и ![]() векторов
векторов ![]() и
и ![]() соответственно и на них, как на сторонах, построим ромб, диагональ которого
соответственно и на них, как на сторонах, построим ромб, диагональ которого ![]() , равную сумме ортов, можно взять в качестве направляющего вектора биссектрисы.
, равную сумме ортов, можно взять в качестве направляющего вектора биссектрисы.
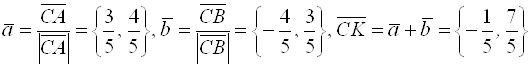 .
.
Каноническое уравнение биссектрисы ![]() примет вид
примет вид  или
или ![]() .
.
Пример 2. Определить при каких значениях ![]() и
и ![]() прямая
прямая ![]() параллельна оси абсцисс и отсекает на оси ординат отрезок, равный
параллельна оси абсцисс и отсекает на оси ординат отрезок, равный ![]() , считая от начала координат.
, считая от начала координат.
Решение. Если прямая параллельна оси абсцисс, то ее нормаль перпендикулярна этой оси, то есть ее первая координата (абсцисса) равна ![]() . Так как
. Так как ![]() , то
, то ![]() . В уравнении
. В уравнении ![]() величина
величина ![]() равна длине отрезка, отсекаемого прямой на оси
равна длине отрезка, отсекаемого прямой на оси ![]() . Перепишем уравнение прямой в виде
. Перепишем уравнение прямой в виде  . Тогда
. Тогда 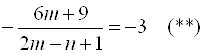 . Решая совместно уравнения (*) и (**), найдем
. Решая совместно уравнения (*) и (**), найдем ![]() ,
, ![]() .
.
Пример 3. Две стороны квадрата лежат на прямых ![]() и
и ![]() . Вычислить его площадь.
. Вычислить его площадь.
Решение. По условию заданы уравнения параллельных сторон. Для нахождения длины стороны квадрата достаточно найти расстояние между прямыми, взяв на одной прямой ![]() какую-нибудь точку, например
какую-нибудь точку, например ![]() , и подсчитать расстояние от точки
, и подсчитать расстояние от точки ![]() до прямой
до прямой ![]() :
:
 . Тогда
. Тогда ![]() .
.
Пример 4. Основанием равнобедренного треугольника служит прямая ![]() , его вершина находится в точке
, его вершина находится в точке ![]() , тангенс угла при основании равен
, тангенс угла при основании равен ![]() . Написать уравнения боковых сторон треугольника.
. Написать уравнения боковых сторон треугольника.
Решение. Из уравнения ![]() находим
находим ![]() . Известно, что
. Известно, что![]()
 .
.![]() Получаем
Получаем 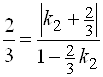 , откуда находим два значения
, откуда находим два значения ![]() и
и ![]() . Подставляя поочередно эти значения в уравнение
. Подставляя поочередно эти значения в уравнение ![]() , где в качестве точки
, где в качестве точки ![]() берется точка
берется точка ![]() , получим два уравнения:
, получим два уравнения: ![]() и
и ![]() .
.
Пример 5. Найти координаты проекции точки ![]() на прямую
на прямую ![]() .
.
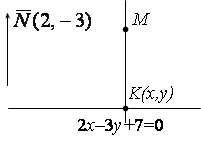 Решение. Точку
Решение. Точку ![]() можно найти как точку пересечения прямых
можно найти как точку пересечения прямых ![]() и
и ![]() . Вектор
. Вектор ![]() является направляющим вектором прямой
является направляющим вектором прямой ![]() , следовательно, ее каноническое уравнение
, следовательно, ее каноническое уравнение  или
или ![]() . Решая систему
. Решая систему  , получим
, получим  ,
, 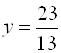 .
.
Пример 6. Найти точку, симметричную точке ![]() относительно прямой
относительно прямой ![]() .
.
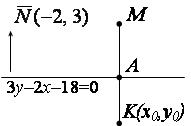 Решение. Уравнение
Решение. Уравнение  запишем в виде
запишем в виде ![]() , откуда
, откуда ![]() может слу-жить направляющим вектором для прямой
может слу-жить направляющим вектором для прямой ![]() . Каноническое уравнение прямой
. Каноническое уравнение прямой ![]() :
:  . Точку
. Точку ![]() найдем как точку пересечения
найдем как точку пересечения![]() Прямых
Прямых ![]() и
и  :
: 
![]() ,
, ![]() ,
,
![]()
![]() .
.
Используя формулу деления отрезка в данном отношении, получим: 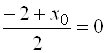 ,
, 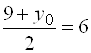 , откуда
, откуда ![]() ,
, ![]() .
.
Пример 7. Найти уравнения касательных к окружности с центром в точке ![]() и радиуса 3, параллельных прямой
и радиуса 3, параллельных прямой ![]() .
.
Решение. У параллельных прямых общая нормаль ![]() , следовательно, уравнения касательных имеют вид
, следовательно, уравнения касательных имеют вид ![]() . Касательные удалены от центра на расстояние
. Касательные удалены от центра на расстояние ![]() , поэтому
, поэтому  , откуда
, откуда ![]() ,
, ![]() . Получаем два уравнения касательных:
. Получаем два уравнения касательных: ![]() и
и 
![]() .
.
Пример 8. Написать уравнение прямой, параллельной прямой ![]() и образующей вместе с осями координат треугольник, площадь которого равна 5.
и образующей вместе с осями координат треугольник, площадь которого равна 5.
Решение. Так как прямые параллельны, то уравнение искомой прямой ![]() . Площадь прямоугольного треугольника
. Площадь прямоугольного треугольника 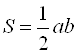 , где
, где ![]() и
и ![]() его катеты. Найдем точки пересечения искомой прямой с осями координат:
его катеты. Найдем точки пересечения искомой прямой с осями координат:
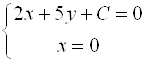
![]()
![]()
 ;
;

 .
.
Итак, ![]() . Подставим в формулу для площади:
. Подставим в формулу для площади: 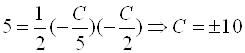 . Получаем два решения:
. Получаем два решения: ![]() и
и ![]() .
.
Пример 9. Даны координаты трех вершин прямоугольной трапеции ![]() :
: ![]() . Составить уравнения всех ее сторон.
. Составить уравнения всех ее сторон.
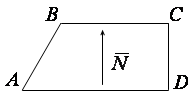 Решение. Зная координаты точек
Решение. Зная координаты точек ![]() и
и ![]() , можно найти
, можно найти ![]() , тогда уравнение
, тогда уравнение ![]() :
: 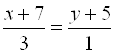 или
или ![]() , нормаль которой
, нормаль которой ![]() служит направляющим вектором прямой
служит направляющим вектором прямой ![]() , поэтому уравнение
, поэтому уравнение ![]() имеет вид
имеет вид  или
или ![]() . Так как прямые
. Так как прямые ![]() и
и ![]() параллельны, то у них общая нормаль, поэтому уравнение
параллельны, то у них общая нормаль, поэтому уравнение ![]() запишем в виде
запишем в виде ![]() или
или ![]() . Уравнение прямой
. Уравнение прямой ![]() можно получить как уравнение прямой, проходящей через две данные точки:
можно получить как уравнение прямой, проходящей через две данные точки: 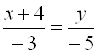 или
или ![]() .
.
Для самостоятельного решения.
1. Даны вершины треугольника ![]() ,
, ![]() ,
, ![]() . Составить уравнение высоты, опущенной из вершины
. Составить уравнение высоты, опущенной из вершины ![]() на сторону
на сторону ![]() .
.
Ответ: ![]() .
.
2. Найти точку, равноудаленную от точек ![]() ,
, ![]() и отстоящую от прямой
и отстоящую от прямой ![]() на расстоянии
на расстоянии ![]() .
.
Ответ: ![]() ,
, ![]() .
.
3. При каком ![]() прямая
прямая ![]() отсекает на оси
отсекает на оси ![]() отрезок
отрезок ![]() ?
?
Ответ: ![]() .
.
4. Из всех прямых, параллельных прямой ![]() , выделить те, которые отсекают от координатных углов треугольники с площадью
, выделить те, которые отсекают от координатных углов треугольники с площадью ![]() .
.
Ответ: ![]() ,
, ![]() .
.
5. Составить уравнения катетов равнобедренного прямоугольного треугольника, если уравнение гипотенузы ![]() и вершина прямого угла
и вершина прямого угла ![]() .
.
Ответ: ![]() ,
, ![]() .
.
6. Даны уравнения оснований трапеции ![]() и
и ![]() . Вычислить длину ее высоты.
. Вычислить длину ее высоты.
Ответ: ![]() .
.
7. Даны три последовательные вершины параллелограмма ![]() ,
, ![]() ,
, ![]() . Составить уравнение диагонали
. Составить уравнение диагонали ![]() .
.
Ответ: ![]() .
.
8. Даны две стороны треугольника ![]() ,
, ![]() и точка пересечения его высот
и точка пересечения его высот ![]() . Составить уравнение третьей стороны треугольника.
. Составить уравнение третьей стороны треугольника.
Ответ: ![]() .
.
9. Через точку пересечения прямых ![]() и
и ![]() провести прямую под углом
провести прямую под углом ![]() к прямой
к прямой ![]() .
.
Ответ: ![]() ,
, ![]() .
.
10. Концами одной диагонали квадрата служат точки ![]() и
и ![]() . Найти уравнения диагоналей и сторон квадрата.
. Найти уравнения диагоналей и сторон квадрата.
Ответ: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
| < Предыдущая | Следующая > |
|---|