2.6 Векторное и смешанное произведения векторов
Определение. Векторным произведением двух ненулевых, неколлинеарных векторов ![]() и
и ![]() называется вектор
называется вектор ![]() обозначаемый
обозначаемый ![]() и удовлетворяющий трем условиям:
и удовлетворяющий трем условиям:
1) ![]() и
и ![]() (то есть
(то есть ![]() перпендикулярен плоскости, определяемой векторами
перпендикулярен плоскости, определяемой векторами ![]() и
и ![]() , если они отложены от одной точки);
, если они отложены от одной точки);
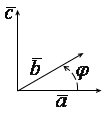 2)
2) ![]() – правая тройка (т. е., если
– правая тройка (т. е., если ![]() приведены к общему началу, то из конца
приведены к общему началу, то из конца ![]() поворот от вектора
поворот от вектора ![]() к вектору
к вектору ![]() на меньший угол виден происходящим против часовой стрелки);
на меньший угол виден происходящим против часовой стрелки);
3) ![]() , где
, где ![]() .
.
Заметим, что все условия в этом определении равноправны, т. е. нельзя отдавать предпочтение какому либо условию или пренебрегать любым из них.
Свойства векторного произведения.
1. ![]() .
.
2. ![]() , где
, где ![]() – скаляр.
– скаляр.
3. ![]() .
.
4. ![]() – равен площади параллелограмма, построенного на приведенных к общему началу векторах
– равен площади параллелограмма, построенного на приведенных к общему началу векторах ![]() и
и ![]() . (Геометрический смысл векторного произведения.)
. (Геометрический смысл векторного произведения.)
5. Для того, чтобы ненулевые векторы ![]() И
И ![]() были коллинеарны, необходимо и достаточно, чтобы
были коллинеарны, необходимо и достаточно, чтобы ![]() . В частности
. В частности ![]() .
.
6. Если заданы декартовы координаты векторов ![]() и
и ![]() , то
, то ![]() можно представить в виде:
можно представить в виде:
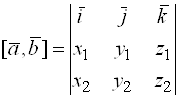 . (13)
. (13)
Определение. Смешанным произведением трех ненулевых, некомпланарных векторов ![]() называется скалярное произведение векторов
называется скалярное произведение векторов ![]() и
и ![]() . Обозначается
. Обозначается ![]() или
или ![]() .
.
Свойства смешанного произведения.
1. Смешанное произведение трех некомпланарных векторов геометрически равно объему параллелепипеда, построенного на этих векторах, взятому со знаком плюс, если ![]() – правая тройка и со знаком минус, если
– правая тройка и со знаком минус, если ![]() – левая тройка.
– левая тройка.
2. Три вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю.
3. ![]() , т. е. смешанное произведение не изменяется при круговой (циклической) перестановке всех сомножителей, а перестановка двух сомножителей меняет знак произведения.
, т. е. смешанное произведение не изменяется при круговой (циклической) перестановке всех сомножителей, а перестановка двух сомножителей меняет знак произведения.
4. Если векторы ![]() заданы декартовыми координатами
заданы декартовыми координатами ![]() ,
, ![]() и
и ![]() , то
, то
 . (14)
. (14)
Пример 26. Найти ![]() , если
, если ![]() ,
, ![]() . В ответе укажите координаты
. В ответе укажите координаты ![]() .
.
Решение. В декартовом базисе векторное произведение ищется по формуле (13):
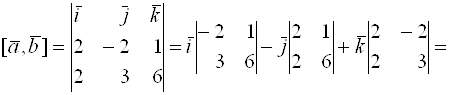
![]() , то есть
, то есть ![]() .
.
Пример 27. Найти ![]() , если
, если ![]() ,
, ![]() .
.
Решение. Поскольку у векторов ![]() И
И ![]() третья координата отсутствует, то можно положить
третья координата отсутствует, то можно положить ![]() ,
, ![]() и применить ту же формулу, что и в предыдущем примере:
и применить ту же формулу, что и в предыдущем примере:
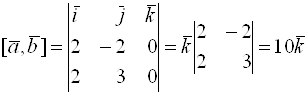 .
.
Пример 28. Найти ![]() , если
, если ![]() ,
, ![]() .
.
Решение. Bекторное произведение ![]() найдено в примере 26, тогда
найдено в примере 26, тогда ![]() .
.
Пример 29. Найти ![]() , если
, если ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Решение. Базис ![]() – аффинный, поэтому формула (13) неприменима.
– аффинный, поэтому формула (13) неприменима.
Найдем ![]() , используя свойства векторного произведения:
, используя свойства векторного произведения: ![]()
![]() . Тогда
. Тогда 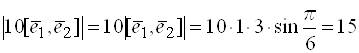 .
.
Пример 30. Вычислить площадь параллелограмма, построенного на векторах ![]() ,
, ![]() , где
, где ![]() ,
, ![]() ,
,  .
.
Решение.
![]() . Так как
. Так как ![]() , а
, а ![]() , то получаем:
, то получаем:
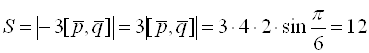 .
.
Заметим, что одной из самых распространенных ошибок является неверное использование геометрического смысла векторного произведения, а именно, полагают, что ![]() . Однако такое равенство лишено смысла, так как в левой его части стоит число, а в правой – вектор.
. Однако такое равенство лишено смысла, так как в левой его части стоит число, а в правой – вектор.
Пример 31. Вычислить ![]() , если
, если ![]() ,
, ![]() ,
, ![]() .
.
Решение. В декартовом базисе смешанное произведение находят с помощью определителя третьего порядка по формуле (14):
 .
.
Пример 32. При каком ![]() , если оно существует, векторы
, если оно существует, векторы ![]() ,
, ![]() и
и ![]() компланарны?
компланарны?
Решение. Для компланарности трех векторов необходимо и достаточно обращение в нуль их смешанного произведения, поэтому 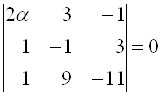 . Раскрывая определитель, получим
. Раскрывая определитель, получим ![]() , откуда
, откуда ![]() .
.
Пример 33. Смешанное произведение ![]() . Найти
. Найти ![]() .
.
Решение. Найдем искомое смешанное произведение, пользуясь его свойствами:
![]()
![]() , так как смешанное произведение, содержащее два одинаковых сомножителя, равно 0, в силу того, что всегда можно так переставить сомножители, что вектор будет умножаться сам на себя векторно, а
, так как смешанное произведение, содержащее два одинаковых сомножителя, равно 0, в силу того, что всегда можно так переставить сомножители, что вектор будет умножаться сам на себя векторно, а ![]() .
.
Пример 34. Даны точки ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Найти:
1) угол, образованный с осью ![]() вектором
вектором ![]() ;
;
2) ![]() ;
;
3) высоту пирамиды ![]() , опущенной из вершины
, опущенной из вершины ![]() .
.
Решение.
1) Угол между векторами мы находить умеем. Поэтому возьмем любой вектор, расположенный на оси ![]() , например,
, например, ![]() , тогда
, тогда 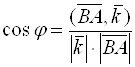 . Находя
. Находя ![]() ,
, ![]() , получим
, получим 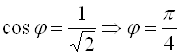 .
.
2) ![]() ,
, ![]() ,
, ![]() . Обозначим
. Обозначим ![]() , тогда
, тогда  .
.
 .
.
3) Из школьного курса геометрии известно, что
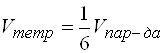 ,
,  , откуда
, откуда 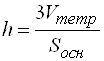 .
.
 Если высота опущена из вершины
Если высота опущена из вершины ![]() , то основанием служит
, то основанием служит ![]() , площадь которого
, площадь которого 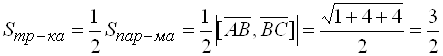 .
.
Найдем объем пирамиды:
 , тогда
, тогда
 .
.
| < Предыдущая | Следующая > |
|---|