2.5 Скалярное произведение векторов

Определение. Скалярным произведением двух ненулевых векторов и называется число, обозначаемое символом , равное произведению их модулей на косинус угла между ними, то есть (в дальнейшем будем обозначать: ).

Если , либо или , то .

Очевидно, что скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда векторы ортогональны.

Свойства скалярного произведения:

1) (переместительное свойство);

2) , где – скаляр; (сочетательное свойство относительно );

3) (распределительное свойство);

4) , если и .

Если , , то

, (6)

Формула (6) справедлива только для декартового базиса.

С помощью скалярного произведения можно находить:

1) длину вектора:

, (в любом базисе); (7)

, (только в декартовом базисе); (8)

2) расстояние между точками и : – cм. формулы (7) и (8);

3) проекцию одного вектора на направление другого:

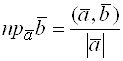, (в любом базисе); (9)

4) косинус угла между векторами:

, (в любом базисе); (10)

5) направляющие косинусы вектора (косинусы углов, которые образует с осями координат:

):

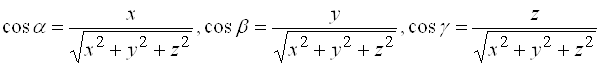; (11)

6) координаты орта вектора :

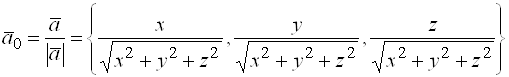. (12)

Так как координаты орта вектора совпадают с его направляющими косинусами и , то .

Чтобы решить любую задачу с применением скалярного произведения векторов, необходимо усвоить разницу в вычислении скалярного произведения в декартовом и в аффинном базисах.

Пример 18. Найти , если .

Решение. По определению скалярного произведения .

Пример 19. Найти , если

.

Решение. Так как и заданы в декартовом базисе, то воспользуемся формулой (6): .

Пример 20. Найти , если , где .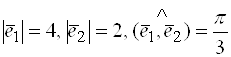

Решение. Здесь векторы и заданы в аффинном базисе, поэтому формулу (6) применять нельзя. Будем считать , используя свойства скалярного произведения:

.

Пример 21. Найти , если .

Решение. Длина вектора в декартовом базисе находится по формуле (8): .

Пример 22. Найти , где , если .

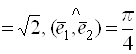Решение. Вектор Задан в аффинном базисе, поэтому применяем формулу (7):

.

Пример 23. Даны векторы и . Найти  и .

Решение. Если базис не указан, то он подразумевается декартовым. Найдем , , . Тогда , .

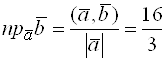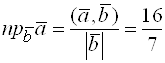Пример 24. Найти , если , , где , , .

Решение. Сначала найдем и , учитывая, что базис – аффинный:

;

.

Тогда .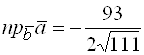

Пример 25. Какой угол образуют единичные векторы и , если известно, что векторы и ортогональны?

Решение. Векторы ортогональны тогда и только тогда, когда их скалярное произведение равно нулю, следовательно , где . Получаем .

< Предыдущая		Следующая >