2.3 Деление отрезка в данном отношении

Пусть точки расположены на одной прямой. Говорят, что точка делит отрезок в отношении , если .

Пусть известны координаты точек и относительно некоторой системы координат: , тогда координаты точки относительно этой же системы координат находятся по формулам:

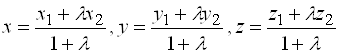. (4)

Если точка находится в середине отрезка , то , то есть и формулы (4) примут вид:

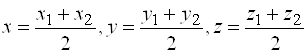. (5)

Пример 15. Треугольник задан координатами своих вершин , , . Найти координаты – точки пересечения его медиан.

Решение. Обозначим через середину , тогда по формулам (5) и 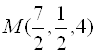. Точка делит медиану в отношении . Применяя формулы (4), находим

.

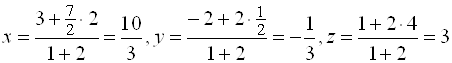Пример 16. Отрезок разделен точкой в отношении , считая от точки . Найти координаты , если .

Решение. Применяя формулы (4), получим:

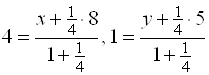, откуда находим .

Пример 17. Отрезок разделен на три равные части точками и . Найти координаты концов отрезка.

Решение. Обозначим , . Точка – середина отрезка , следовательно, по формулам (5) находим: откуда . Аналогично находятся координаты точки (рекомендуется проделать самостоятельно): .

< Предыдущая		Следующая >