16.09. Гомоморфизмы. Фактор-группа

Пусть G – группа с элементами A, B, C, … и – некоторое множество с элементами в котором введена операция: .

Def: Отображение F группы G на множество : Называется гомоморфизмом, если выполнено соотношение F(A×B) = F(A)×F(B). При этом называется гомоморфным образом группы G.

Если , то гомоморфизм Называется эндоморфизмом.

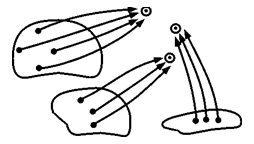Если задано гомоморфное отображение G на , то все элементы группы G разбиваются на непересекающиеся классы; B классы объединяются все те элементы группы G, которые отображаются в один и тот же элемент множества .

Т°. Гомоморфный образ группы есть группа.

◀ Пусть элементы гомоморфного образа группы G при гомоморфизме F. Значит, такие, что Тогда операции в G и согласованны (по определению гомоморфизма) и осталось проверить свойства операции:

А) = F(A)((F(B)×F(C)) = F(A)F(Bc) = F(A(Bc)) = F((Ab)C) = F(Ab)×F(C) = (F(A)F(B))×F(C) =

(ассоциативность операции);

Б) F(E) обозначим : = F(A)F(E) = F(Ae) = F(A) = (т. к. F(E) = единичный элемент);

Б) F(A-1) обозначим : = F(A)F(A–1) = F(A)F(A–1) = F(E) = (т. е. обратный К ) ▶

Пусть H – нормальный делитель группы G. Определим отображение F группы G на множество смежных классов по нормальному делителю Н: F: AÎG, то A ↦AH: AHÎ.

Т°. Отображение F группы G на смежные классы по нормальному делителю Н, при

определении операции умножения классов смежности, как подмножеств группы

G, представляет собой гомоморфизм.

◀ Истинность этого факта следует из доказанной теоремы о том, что произведение смежных классов есть смежный класс ▶

Следствием двух последних теорем является:

Т°. Множество смежных классов группы G по нормальному делителю Н с

операцией умножения этих классов, определенной как произведение подмножеств группы G, образуют группу.

Эта группа Называется фактор-группой группы G по нормальному делителю Н и обозначается: G/H.

Очевидно, отображение F группы G на множество смежных классов по нормальному делителю Н представляет собой гомоморфизм этой группы на фактор-группу G/H.

Пример: Пусть Rn – N-мерное линейное пространство. Оно является абелевой группой по сложению. По определению прямого произведения . –абелева подгруппа, т. е. нормальный делитель группы Rn. Смежным классом AÎRn служат многообразие , фактор-группа Rn/ изоморфна (N–1) – подпространству Rn–1: т. е. Rn–1 = Rn/. Кстати, именно этим и объясняется термин: нормальный делитель и обозначение G/H.

< Предыдущая		Следующая >