09.1. Линейные и полуторалинейные формы в унитарном пространстве. Специальное представление линейных форм

Пусть V – унитарное пространство. Пусть "XÎV ® F(X)ÎC, такое что:

1) F(X1 + X2) = F(X1) + F(X2);

2) F(aX) = aF(X).

Тогда говорят, что из V в C задан линейный функционал F или линейная форма F (FÎL(V, C)).

T°. Пусть FÎL(V, C), т. е. F – линейная форма, тогда существует единственный HÎV

такой, что F(X) = (X, H).

◀ Пусть {EI} – ортонормированный базис V

"XÎV; ,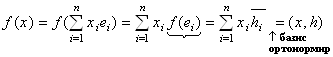

Т. е. вектор H имеет координаты .

Единственность: Пусть F(X) = (X, H1) = (X, H2) Þ (X, H1 – H2) = 0; "XÎV. Возьмем X = H1 – H2 Þ (H1 – H2, H1 – H2) = 0, т. е. H1 = H2 ▶

Примечание: в вещественном пространстве теорема и ее доказательство также справедливы, но в доказательстве не ставится знак комплексного сопряжения.

< Предыдущая		Следующая >