07.3. Связь линейных операторов с матрицами

Пусть А – линейный оператор на V, а Базис V. Тогда "ХÎV .

= .

Таким образом действие оператора А на "ХÎV Полностью определяется числами (Аij) образующими матрицу которая называется матрицей линейного оператора А.

Преобразование, проведенное выше, указывает и способ построения матрицы линейного оператора в заданном базисе. Подействуем линейным оператором на векторы базиса, получившиеся векторы разложим в том же базисе и коэффициенты разложения запишем в соответствующие столбцы матрицы линейного оператора.

1°. В заданном базисе между квадратичными матрицами и линейными операторами существует взаимно однозначное соответствие.

Пример. Найти матрицу линейного оператора в пространстве функций вида {ACos(T + a)} в базисе E1 = cosT, E2 = sinT.

Подействуем оператором А на Еi , полученный вектор разложим в базисе {cosT, sinT} и координаты этого вектора запишем в I-й столбец: 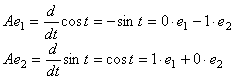. Тогда . Это и есть матрица линейного оператора .

В самом деле: (3cos(T + 5))¢ = ?

3cos(T+ 5) = 3cos5cosT – 3sin5sinT = 3cos5E1 – 3sin5E2.

Тогда .

У = –3sin5E1 – 3cos5E2 = –3sin5cosT – 3cos5sinT = –3sin(T+ 5).

< Предыдущая		Следующая >