06.4. Канонический вид квадратичных форм
Учитывая, что элементы матрицы квадратичной формы Aij = j(Ei, Ej) мы можем заключить, что элементы матрица квадратичной формы зависят от выбора базиса.
Если для формы j(Х, Х) в пространстве V существует базис 
в котором матрица j(Х, Х) имеет диагональный вид (т. е. Aij = 0 Для i ¹ J), и следовательно форма j(Х, Х) записывается так 
то такой базис Называется каноническим базисом J(Х, Х) в пространстве V а запись формы в этом базисе называется каноническим видом формы.
Постановка Задачи: Для формы j(Х, Х) ¹ 0 найти базис, в котором форма имеет канонический вид.
Метод Лагранжа (метод выделения полных квадратов) приведения формы к каноническому виду.
Пусть в некотором базисе 
форма имеет вид: 
.
1). Пусть Aii = 0 ("I), но $Aij ¹ 0. Не ограничивая общности можно считать, что А12 ≠ 0. Тогда 
и получим 
(в записи формы появились члены, содержащие квадраты координат).
2). $Aii ¹ 0. Допустим, что А12 ≠ 0. Тогда:
.
При этом: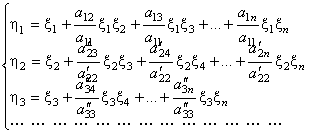 
.
Связь между координатами ξI и ηI позволяет установить векторы нового базиса .
Пример:
=
= 
=
= 
.
При этом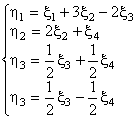 
, т. е. 
.
Векторы нового базиса Е1, е2, Е3, е3, получаются из старых F1, f2, F3, F4 так:
E1 = F1; E2 = 3F1 + 2F2; e3 = –2F1 + 0,5F3 + 0,5F4; e4 = 0,5F3 – 0,5F4.
Метод Якоби приведения формы к каноническому виду.
Пусть форма j(X, X) в базисе 
имеет матрицу А, где AiK = j(Fi, FK); и, при этом, главные миноры матрицы квадратичной формы отличны от нуля: D1¹0, D2¹0, D3¹0, …, DN = detA ¹0 . Форма j(X, X) в базисе имеет вид: j(X, X) =
. Требуется найти базис {E1, E2, …, En}, чтобы j(Ei, Ek) = 0 (I ¹ K). Векторы канонического базиса {E1, E2, …, En}, ищем из соотношений:
. (1)
При этом, нетрудно заметить, что ℒ(Е1, е2, …, еn) = ℒ(F1, f2,…, fn). Отметим, что если j(Ek, Fi) = 0, I = 1, 2, …, K –1, то j(Ei, Ek) = 0 I = 1, 2, …, K –1. В счамом деле
J(Ei, Ek) = j(Ek, aI1F1 + aI2F2 + … + aIiFi) = 0.
Тогда коэффициенты aIj Будем искать из соотношений:
J(Ek, Fi) = 0 (J < K)
J(Ek, Fk) = 1. (*)
Тогда для коэффициентов разложения: Ek = aK1F1 + aK2F2 + aK3F3 +…+ aKnFn Из условий (*),
Получим систему уравнений :
J (Ek,F1) = aK1j (F1,F1) + aK2 j (F2,F1) + aK3 j (F3,F1) + … … … + aKk J (Fk,F1) = 0
J (Ek,F2) = aK1j (F1,F2) + aK2 j (F2,F2) + aK3 j (F3,F2) + … … … + aKk J (Fk,F2) = 0
… … … … … … … … … … … … … … … … … … … … … … … …
J (Ek,Fk-1) = aK1j (F1,Fk-1) + aK2 j (F2,Fk-1) + aK3 j (F3,Fk-1) + … … + aKk J (Fk,Fk-1) = 0
J (Ek,Fk) = aK1j (F1,Fk) + aK2 j (F2,Fk) + aK3 j (F3,Fk) + … … … … + aKk J (Fk,Fk) = 1
Полученная система линейных уравнений имеет единственное решение, ибо ее определитель ΔK ¹ 0. При этом получим, что: j(Ek, Ei) = 0 (K < I), и j(Ek, Ek) ¹ 0.
Запишем:
j (Ek,Ek) = aK1j (Ek,F1) + aK2 j (Ek,F2) + aK3 j (Ek,F3) + … + aKk-1 j (Ek,Fk-1) + aKk J (Ek,Fk) = aKk.
Найти aKk можем из системы уравнений, которая записана выше, по правилу Крамера:
aKk =
. Таким образом, форма j(X, X) в базисе 
имеет канонический вид:
j(X, X) =
, где a11=
, a22=
, a33=
, …, aNn=
. Здесь D0 = 1.
Пример приведения квадратичной формы к каноническому виду методом Якоби.
Пусть форма: 
задана в базисе F1(2, 0, 0), F2(0, 1, 0), F3(0, 0, 1), а полярная ей билинейная форма имеет вид:
.
Матрица билинейной формы и соответствующей ей квадратичной формы равна: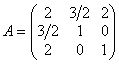 
И ее главные миноры: D1 = 2; D2 = –1/4; D3 = –17/4. Векторы Е1, Е2, Е3 ищем в виде:
E1 = a11F1 = ( a11,0,0 ), E2 = a21F1 + a22F2 = (a21, a22, 0), E3 = a31F1 + a32F2 + a33F = (a31, a32, a33).
Получаем:
А) j(E1, F1) = 1 Þ 2a11 = 1 ® a11 = 
Þ E1
;
Б) 
Þ Е2(6, –8, 0);
В) 
Þ
Þ
.
Получены векторы канонического базиса:
E1 = F1; Е2(6, –8, 0) = 6F1 – 8F2; = 
(8F1 –12F2 + F3)
И в этом базисе форма j(Х, Х) имеет канонический вид:
.
| < Предыдущая | Следующая > |
|---|
