04.07. Свойства определителей
6°. detA = detAT.
◀ 
. ▶
Из этого свойства следует, что строки и столбцы в определителе равноправны. И все свойства для столбцов будут справедливы для строк и наоборот. Все последующие свойства сформулированы для столбцов матрицы, но * у слова столбец означает, что вместо этого слова можно написать слова строка.
7°. Если один из столбцов* определителя равен нулю, то определитель равен нулю.
◀ j(X1, …, θ , …, Xn) = j(X1, …, 0×Хk, …, Xn) = 0×j(X1, X2, …, Xn) = 0. ▶
8°. 
.
◀ j(X1, X2, …, Xk´ + Xk, …, Xn) = j(X1, X2, …, Xk´, …, Xn) + j(X1, X2, …, Xk, …, Xn). ▶
9°. Общий множитель в столбце * определителя можно выносить за знак определителя.
◀ j(X1, X2, …, aXk, …, Xn) = aj(X1, X2, …, Xk, …, Xn). ▶
10°. Если в определителе поменять два столбца * местами определитель поменяет знак.
◀ j(X1, …, Xe,…, Xm, …, Xn) = – j(X1, …, Xm, …, Xe, …, Xn). ▶
11°. Определитель, имеющий два равных столбца * равен нулю.
◀ Действительно, если поменять местами два столбца, то detA не изменится, ибо они одинаковы, а с другой стороны detA поменяет знак из-за антисимметричности. Следовательно, detA = 0. ▶
12°. Если столбцы* матрицы линейно зависимы, то detA = 0.
◀ Пусть Х1 = 
. Тогда j(X1, X2, …, Xn) =
= 
= 0. ▶
Если в матрице Am´N зафиксировать к строк и к столбцов (K ≤ min(M, N)), то определитель K-порядка матрицы из элементов Am´N, стоящих в выбранных строках и столбцах называются минором K-порядка.
Если у detA порядка N, вычеркнуть I-ю строку и J-й столбец, то оставшиеся элементы образуют матрицу (N – 1) порядка. Ее определитель – минор (N – 1)го порядка и обозначается Mij, а величина Aij = (–1)I+JMij Называется алгебраическим Дополнением к элементу Аij.
13°. 
.
◀ 
=
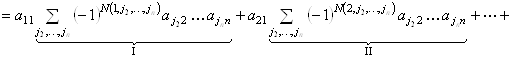
I. 
;
II. 
;
….. ….. ….. ….. ….. ….. ….. ….. ….. ….. ….. ….. ….. …..
N. 
.
Следовательно: detA= … = A11A11 + A21A22 + … + An1An1. ▶
Это все можно проделать не только для первого столбца, а и для 2го, 3го, … , NГо столбцов и аналогично для строк.
14°. 
.
◀ 
. ▶
15°. Определитель матрицы не изменится, если к столбцу * добавить линейную комбинацию других столбцов *.
◀ j(X1 + a2X2 + … + aNxn, X2, … , Xn) = j(X1, X2, …, Xn) + a1j(X2, …, Xn) + a3(X3, X2, …, Xn) +
+ aN(Xn, X2,…, Xn) = j(x1,x2,…,xn ) . ▶
16°. При умножении матрицы на a, ее определитель умножается на aN : det(AA) = aN DetA.
◀ j(aX1, aX2 , … , aXn) = a×a … aj(X1, X2, …, Xn) = aNJ(X1, X2, …, Xn). ▶
17°. Определитель произведения двух матриц произведению определителей сомножителей detA×B = detC = detA ×detB. (C = A×B Û Сij = 
).
◀ detC = 
= 
=
= 
. ▶
| < Предыдущая | Следующая > |
|---|
