04.06. Определитель квадратной матрицЫ

Пусть задана квадратная матрица .

Определителем (detA) квадратной матрицы А со столбцами Xi = Называется функционал j(X1, X2, …, XN) относительно столбцов этой матрицы, которой а) линеен по каждому аргументу (полилинеен);

б) абсолютно антисимметричен (антисимметричен по любой паре аргументов);

в) выполнено условие нормировки .

Таким образом:

5°. .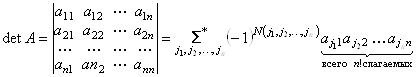

Например: для определителя 3го порядка В сумму входят 3! слагаемых A11A22A33, A12A23A31, A13A21A32, A13A22A31, A12A21A33 и A11A23A32. Знаки этих слагаемых определяются четностью перестановок: , , , , , . Количество беспорядков в этих перестановках соответственно равно: 0, 2, 2, 3,1,1. Первые три перестановки четные, последние три нечетные, поэтому получаем уже известную из курса аналитической геометрии формулу:

= A11A22A33 + A12A23A31 + A13A21A32 – A13A22A31 – A12A21A33 – A11A23A32.

Аналогично можно выписать непосредственно формулу вычисления определителя 4го порядка (24 слагаемых), 5го порядка (120 слагаемых). Ясно, что с увеличением порядка определителя его вычисление по определению становится чрезвычайно обременительным, если не невозможным.

Изучение свойств определителей позволит нам обойти эту трудность.

< Предыдущая		Следующая >