02.12. Ортогональная проекция и ортогональная составляющая вектора на подпространство
Пусть L – подпространство евклидового или унитарного пространства V. Тогда "XÎV $X0ÎL Ù $X^ÎL^ (причем единственные), такие что X = X0 + X^, X0 – Называется ортогональной проекцией вектора Х на подпространство L. X^ – Называется ортогональной составляющей вектора Х на подпространство L. Расстоянием Между двумя множествами M1 и M2 Называется кратчайшее из расстояний между элементами M1 и M2: r(M1, M2) = ![]() .
.
 В частности r(X, M) =
В частности r(X, M) = ![]() ; r2(X, Y) = |X – Y|2 =
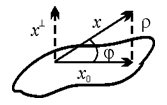
; r2(X, Y) = |X – Y|2 = ![]() = |X – X0|2 + |X0 – Y|2 ³ ³ | X – X0 |2 = | X^ |2, где YÎL, т. е. Расстоянием между вектором и подпространством является длина его ортогональной составляющей. Для евклидового пространства углом между вектором Х и подпространством L Называется угол jÎ[0, p] такой, что
= |X – X0|2 + |X0 – Y|2 ³ ³ | X – X0 |2 = | X^ |2, где YÎL, т. е. Расстоянием между вектором и подпространством является длина его ортогональной составляющей. Для евклидового пространства углом между вектором Х и подпространством L Называется угол jÎ[0, p] такой, что ![]() .
.
Преобразовав  , получим, что косинус угла между подпространством и вектором равен отношению длины ортогональной составляющей вектора к длине самого вектора.
, получим, что косинус угла между подпространством и вектором равен отношению длины ортогональной составляющей вектора к длине самого вектора.
Рассмотрим ![]() – ортогональный базис в подпространстве L:
– ортогональный базис в подпространстве L:
"XÎV X = X0 + X^ = a1E1 + a1E1 + … + aKEk + X^.
Умножим скалярно обе части равенства на Ei:
![]() , т. е.
, т. е.
 – это формулы для нахождения ортогональной проекции и ортогональной составляющей вектора Х на подпространство L.
– это формулы для нахождения ортогональной проекции и ортогональной составляющей вектора Х на подпространство L.
| < Предыдущая | Следующая > |
|---|