01.22. Ещё действия над матрицами

А) Произведение матриц Сnk = AnmBmk определим по правилу: Cij = (это правило в обиходе называется: умножение строка на столбец).

Пример: 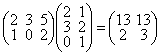, но . Из определения произведения матриц ясно, что матрицы можно умножать не всегда, а только если количество элементов в строке 1ой матрицы и количество элементов в столбце 2ой матрицы совпадают. Кроме того, видно, что операция умножения матриц, вообще говоря, не коммутативна.

Можно отметить следующие свойства операции умножения матриц:

А1) А(ВС) = (АВ)С – ассоциативный закон;

А2) А(В + С) = АВ + АС – левый и

А3) (А + В)С = АС + ВС правый дистрибутивные законы.

Def: Если в линейном пространстве V над полем К, корректным образом, введена еще одна внутренняя операция, удовлетворяющая свойствам:

1) a⊙(Х⊗У) = (a⊙Х)⊗У = Х⊗(a⊙у);

2) Х⊗(У⊗Z) = (Х⊗У)⊗Z; 3) (Х ⊕ У)⊗Z = Х⊗Z ⊕ У⊗Z,

То линейное пространство над полем К называется алгеброй.

Таким образом, определив операцию умножения матриц, удовлетворяющую свойствам а1), а2), а3) мы можем говорить об алгебре матриц (для квадратных матриц).

Б) Транспонирование матриц АТ Û = Аji.

Пример: .

Свойства операции транспонирования:

Б1) (aА)Т = aАТ;

Б2) (А + В)Т = АТ + ВТ;

Б3) (А×В)Т = АТВТ.

В) Для матриц с комплексными элементами – операция комплексного сопряжения. .

Г) Для матриц с комплексными элементами – операция эрмитового сопряжения. (для операции эрмитового сопряжения, математики чаще употребляют значок А*, а физики А+).

Свойства операции эрмитового сопряжения:

Г1) ; г2) ; г3) ;

Г4) ; г5) .

Примеры: ; ; ; .

Элементы А11, А22, …, Ann – Называются диагональными (главными диагональными) элементами матрицы.

Если "I > J aij = 0 Матрица называется матрицей нижнего треугольного вида, если "I < J aij = 0 – Матрицей верхнего треугольного вида: ; .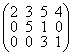

нижний верхний

Треугольный треугольный

вид вид

Примечание: Если А* = А, то Матрица называется эрмитовой (Самосопряженной).

В вещественном пространстве матрица А, удовлетворяющая условию: ААТ = АТА = Е Называется ортогональной, а комплексном пространстве – Унитарной.

< Предыдущая		Следующая >