5.2. Методы уточнения решений СНУ. Метод простых итераций
Уточнение интересующего решения до требуемой точности ε производится итерационными методами.
Основные методы уточнения решений СНУ получены путем обобщения итерационных процессов, используемых при решении одного нелинейного уравнения.
Как и в случае одного уравнения, метод простых итераций заключается в замене исходной системы уравнений (5.1) эквивалентной системой
X=Φ(X) (5.3)
И построении итерационной последовательности
X(k) = Φ(X(k-1)) , где k=1,2,3,… - номер итерации, (5.4)
Которая при k→∞ сходится к точному решению.
Здесь - итерирующая вектор-функция, X(0) 
D – начальное
Приближение решения.
В развернутом виде формула итерационного процесса (выражение для вычисления очередного k-го приближения решения) имеет вид:
Xi.(k) = φi(x1(k-1), x2(k-1), … , xn(k-1)), 
. (5.5)
Условие окончания расчета
δ≤ε (5.6)
Где ε - заданная точность решения;
δ = 
(5.7)
Или
δ =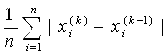 
(5.8)
Итерационный процесс (5.5) сходиться к точному решению, если в окрестности решения соблюдаются условия сходимости:
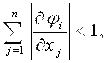
(5.9)
Или
(5.10)
Таким образом, для уточнения решения СНУ методом простых итераций нужно найти такое эквивалентное преобразование (5.1) в (5.3), чтобы в области существования решения выполнялись условия (5.9) или (5.10).
В простейшем случае эквивалентную систему можно получать как:
, 
Можно выделить (не обязательно явно) все неизвестные из уравнений системы так, что:
,
Как и в случае одного уравнения задачу поиска эквивалентного преобразования можно свести к задаче определения (в простейшем случае подбора) значений констант li ≠ 0, , обеспечивающих сходимость
Рис. 5.1. Схема алгоритма метода простых итераций.
|
использовать уже найденные значения 
Выражение для расчета очередного к-го приближения примет вид:
, ; (5.11)
Для реализации данного приема, аналогичного методу Гаусса-Зейделя для систем линейных уравнений, в алгоритм расчета следует внести изменения: формулу расчета очередного приближения (символ 5) записать как X=φ(x) или в развернутом виде:
,
Существуют и другие приемы улучшения сходимости метода простых итераций. Например, новое приближение вычислять как среднее арифметическое двух предшествующих приближений:
, (5.12)
Можно использовать поправку Эйткена для улучшения сходимости:
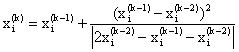, (5.13)
Пример 5.2.
Методом простых итераций уточнить ранее (пример 5.1) отделенные решения системы уравнений:
X12+x22=1
Ln x1+2x2= –1
Области существования решений:
, 
Для получения эквивалентной системы из первого уравнения выразим x1
Из второго уравнения x2
Определим частные производные:
Проверим условия сходимости в окрестности первого решения, взяв точку в центре области существования этого решения х1=0,1; х2=0,9.
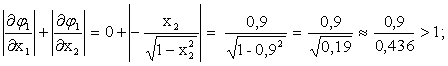
Использовать полученную эквивалентную систему для уточнения первого решения нельзя, т. к. условия сходимости не соблюдаются.
Проверим условия сходимости для этой же эквивалентной системы в окрестности второго решения: х1=0,9; х2=-0,4.
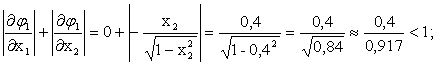
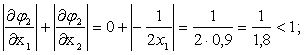
Условия сходимости соблюдаются, следовательно полученную эквивалентную систему можно использовать для уточнения второго решения.
Выполним несколько итераций для уточнения 2-го решения:
Начальные значения k = 0 
; 
;
Первая итерация k = 1 
;
Вторая итерация k = 2 
;
Третья итерация k = 3 
Четвертая итерация k = 4 
Итерационный процесс сходиться, для достижения требуемой точности нужно выполнить еще несколько итераций.
После 8-ой итерации х1=0,8956, х2=-0,4446, δ по формуле (5.7) равна 0,0005.
Рассмотрим использование приема Гаусса–Зейделя (5.11) для ускорения итерационного процесса.
Начальные значения k = 0, 
; 
;
Первая итерация k = 1 ;
Вторая итерация k = 2 
;
После 5 итерации получим следующие результаты: х1=0,8957, х2=-0,4449 δ=0,0006.
Для уточнения первого решения нужно найти другую формулу итерационного процесса.
Например, если из первого уравнения выразить х2, а из второго х1 получим:
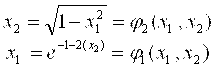
Проверка условий сходимости в окрестности первого решения показывает, что приведенные формулы можно использовать для уточнения первого решения.
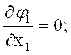
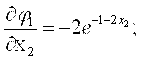
Для х(0)=(0,1;0,9)
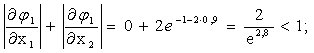
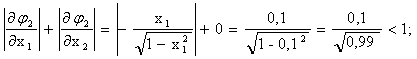
| < Предыдущая | Следующая > |
|---|
