5.2.1. Метод Ньютона–Рафсона
Идея метода заключается в линеаризации уравнений системы (5.1), что позволяет свести исходную задачу решения СНУ к многократному решению системы линейных уравнений.
Рассмотрим, как были получены расчетные зависимости метода.
Пусть известно приближение xi(k) решения системы нелинейных уравнений xi*. Введем в рассмотрение поправку Dxi как разницу между решением и его приближением:
![]() ,
, ![]()
Подставим полученное выражение для xi* в исходную систему.
![]()
![]()
![]()
…
![]()
Неизвестными в этой системе нелинейных уравнений являются поправки Dxi. Для определения Dxi нужно решить эту систему. Но решить эту задачу так же сложно, как и исходную. Однако эту систему можно Линеаризовать, и, решив ее, получить Приближенные значения поправок Dxi для данного приближения, т. е. Dxi(k). Эти поправки не позволяют сразу получить точное решение ![]() , но дают возможность приблизиться к решению, – получить новое приближение решения
, но дают возможность приблизиться к решению, – получить новое приближение решения
![]() ,
, ![]() (5.14)
(5.14)
Для линеаризации системы следует разложить функцию fi в ряды Тейлора в окрестности xi(k), ограничиваясь первыми дифференциалами.
Полученная система имеет вид:
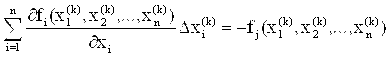 ,
, ![]() (5.15)
(5.15)
Все коэффициенты этого уравнения можно вычислить, используя последнее приближение решения xi(k). Для решения системы линейных уравнений (5.15) при n=2,3 можно использовать формулы Крамера, при большей размерности системы n – метод исключения Гаусса.
Значения поправок используются для оценки достигнутой точности решения. Если максимальная по абсолютной величине поправка меньше заданной точности e, расчет завершается. Таким образом, условие окончания расчета:
δ = ![]()
Можно использовать и среднее значение модулей поправок:
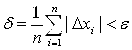
В матричной форме систему (5.15 ) можно записать как:
![]() (5.16)
(5.16)
Где:
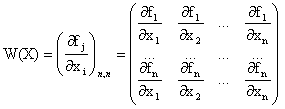 , - матрица Якоби (производных),
, - матрица Якоби (производных),
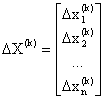 - вектор поправок
- вектор поправок
![]() - вектор-функция
- вектор-функция
W(X(k)) – матрица Якоби, вычисленная для очередного приближения.
F(X(k)) – вектор-функция, вычисленная для очередного приближения.
Выразим вектор поправок ∆X(k) из (5.16):
![]()
Где W-1 – матрица, обратная матрице Якоби.
Окончательно формула последовательных приближений метода Ньютона решения СНУ в матричной форме имеет вид:
![]() (5.17)
(5.17)
Достаточные условия сходимости для общего случая имеют очень сложный вид, и на практике проверяются редко. Нужно отметить, что метод сходится очень быстро (за 3 – 5 итераций), если det|W| ¹ 0 и начальное приближение X(0) выбрано близким к решению (отличаются не более чем на 10%).
Алгоритм решения СНУ методом Ньютона состоит в следующем:
1. Задается размерность системы n, требуемая точность ε, начальное приближенное решение X = (xi)n.
2. Вычисляются элементы матрицы Якоби W = (¶¦i ¤ ¶xj)n, n.
3. Вычисляется обратная матрица W-1.
4. Вычисляется вектор функция F=(fi)n, ![]() ,
, ![]() .
.
5. Вычисляются вектор поправок ![]()
6. Уточняется решение ![]()
7. Оценивается достигнутая точность δ=![]() или
или 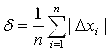
8. Проверяется условие завершения итерационного процесса
δ≤ε
Если оно не соблюдается, алгоритм исполняется снова с пункта 2.
Для уменьшения количества арифметических действий Рафсон предложил не вычислять обратную матрицу W-1, а вычислять поправки как решение СЛУ (5.15)
![]()
Схема алгоритма метода Ньютона - Рафсона представлена на рис.5.2. При разработке схемы учтена необходимость защиты итерационного цикла от зацикливания: введен счетчик итераций k и ограничение на число итераций kmax (на практике не более 100).
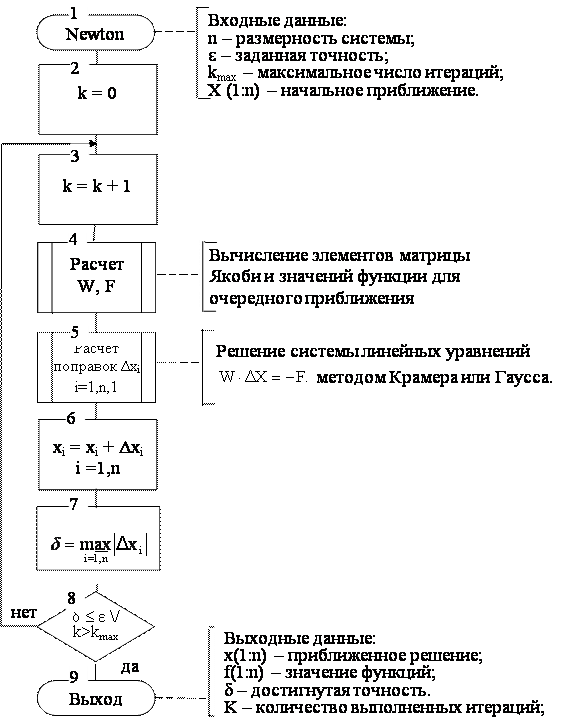 |
Рис 5.5. Схема алгоритма решения СНУ методом Ньютона – Рафсона.
Достоинством методов Ньютона является быстрая сходимость, недостатками - сложность расчетов (вычисление производных, многократное решение системы линейных уравнений), сильная зависимость от начального приближения.
Пример 5.3. Требуется методом Ньютона-Рафсона уточнить одно из решений системы
![]() x12+x22=1
x12+x22=1
Ln x1+2x2= –1
Заданная точность ε=0,001. Решения отделены ранее (пример 5.1)
![]()
Запишем уравнения в стандартном виде:
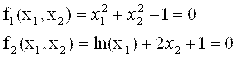
Начальное приближение Х(0)=(0,9;-0,4).
Первая итерация.
Элементы матрицы Якоби W=(wi, j)2,2
W1,1=![]()
W1,2=![]()
W2,1=![]()
W2,2=![]()
Значение функций
F1(0,9;-0,4) = 0,92 + 0,42 – 1 = 0,81+ 0,16 – 1 = -0,03
F2(0,9;-0,4) = ln(0,9) + 2*(-0,4) + 1 = -0,1054 + 0,2 + 1 = 0,0946
Для вычисления поправок нужно решить систему
![]() 1,8×∆x1 - 0,8×Dx2= -(-0,03)
1,8×∆x1 - 0,8×Dx2= -(-0,03)
1,1111×∆x1 + 2×∆x2= –0,0946
По формулам Крамера
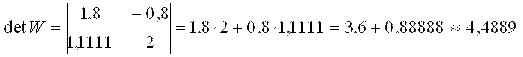
DetW≠0 – система обусловлена.
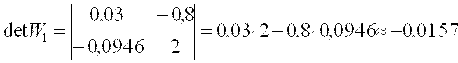
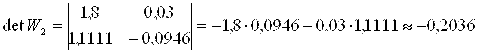
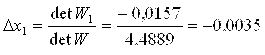
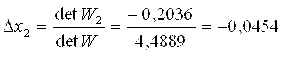
Первое приближение решения
Х1 = х1 + ∆х1 = 0,9+(-0,0035) = 0,8965
Х2 = х2 + ∆х2 = -0,4 + (-0,0454) = -0,4454
Оценка достигнутой точности
![]()
Нужно продолжить итерационный процесс т. к. δ>ε.
После второй итерации требуемая точность достигается, х1=0,8995 х2=-0,4449, d » 0,001.
| < Предыдущая | Следующая > |
|---|