5. Степенная функция
Пусть требуется найти аппроксимирующую функцию в виде степенной:
F(x, a,m) = axm. (3)
При условии, что a>0 и в заданной таблице значения аргумента и значения функции положительны, прологарифмируем равенство (3):
LnF = lna+mlnx.
Введем следующие обозначения u = lnx; A= m; B= lna, тогда lnF будет функцией от u: Ф(u, A,B) = Au+B. Таким образом, нахождение параметров степенной функции мы свели к нахождению параметров линейной функции. Поэтому дальнейшее решение поставленной задачи будет аналогично первому случаю.
Так как частные производные функции Ф(u, A,B) по параметрам А, В: ![]()
![]() То система (2) примет вид:
То система (2) примет вид:
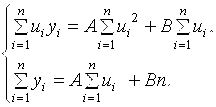
Решив систему, получим значения параметров А, В линейной функции Ф(u, A,B). Сделав обратную замену: a = eB, m = A, получим требуемые параметры степенной функции F(x, a,m )= axm.
Пример № 2. Имеем функцию, заданную таблично.
|
X |
2,3 |
1,56 |
1,3 |
1 |
0,69 |
0,47 |
0,38 |
0,28 |
0,25 |
0,19 |
|
Y |
0,16 |
0,22 |
0,28 |
0,34 |
0,5 |
0,81 |
1,06 |
1,38 |
1,81 |
2,66 |
Представим функцию графически, чтобы выбрать вид зависимости (рис.1).
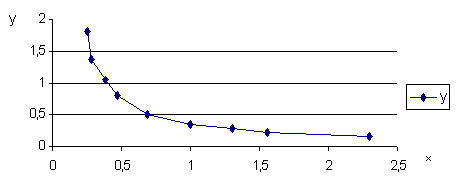
Рис. 1
Найдем аппроксимирующую функцию в виде степенной:
F(x, a,m )= axm
Введем следующие обозначения u= lnx; A = m; B = lna, тогда lnF будет функцией от u : Ф(u, A,B) = Au+B.
Решив систему уравнений, мы найдем коэффициенты A, B:

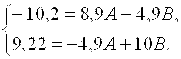
Откуда А = - 0,88, В = 0,49.Сделав обратную замену a = eB, m = A, получим: m = -0,88, a = 1,63. Тогда искомая функция примет вид: F(x, a,m)=1,63x-0.88.
Пусть требуется найти приближающую функцию в виде логарифмической:
F(x, a,b) = a lnx+b.
Так как частные производные функции F(x, a,b) по параметрам a и b равны: ![]()
![]() , то система (2) примет вид:
, то система (2) примет вид:

Откуда получим: 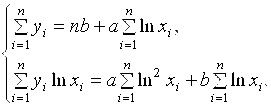
После элементарных преобразований найдем требуемые параметры.
Пример № 3. Имеем функцию заданную, таблично.
|
X |
0.25 |
0.5 |
0.75 |
1.25 |
2.75 |
4.75 |
6.5 |
9.67 |
13.67 |
|
Y |
-7,75 |
-5.8 |
-2.67 |
1.5 |
3.5 |
5.2 |
7.2 |
8.5 |
9.67 |
Представим функцию графически, чтобы выбрать вид аппроксимирующей функции (рис. 2).
![]()
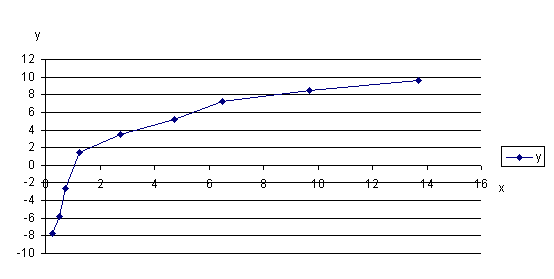
Рис. 2
Найдем аппроксимирующую функцию в виде логарифмической: F(x, a,b) = alnx+b.
Решив систему уравнений, мы найдем коэффициенты а и b:
 ;
;
Где n = 9, из первого уравнения: b = 2,15-0,79a, подставив b во второе уравнение системы, получим:85,56 = 21,48a+7,18 откуда а = 3,73 и b = - 0.79.Тогда искомая функция примет вид: F(x, a,b) = 3,73 lnx - 0,79.
Мы рассмотрели частные случаи нахождения аппроксимирующих функций в виде линейной, квадратичной, степенной, логарифмической функций, параметры других функций вычисляются аналогично.
| < Предыдущая | Следующая > |
|---|