4. Метод наименьших квадратов
Пусть в результате эксперимента получена таблица некоторой функции
|
X |
X1 |
X2 |
X3 |
… |
Xn |
|
F(x) |
Y1 |
Y2 |
Y3 |
… |
Yn |
Требуется найти функцию вида y = F(x), которая в точках x1,x2,…,xn принимает значения, наиболее близкие к табличным значениям y1,y2,…,yn. Такую формулу называют эмпирической формулой или уравнением регрессии y на x, саму функцию называют приближающей функцией или аппроксимирующей.
На практике эту приближающую функцию находят следующим образом. По таблице строят точечный график функции F, по которому устанавливают вид приближающей функции. В качестве приближающей функции y = F(x) в зависимости от характера точечного графика часто используют следующие функции:
Y=ax+b; y=ax2+bx+c; y=axm;
Y=b ax; y=a+b sinx; y=a lnx+b;
Y=1/(ax+b); y=a/x+b; y=x/(ax+b),
Y=a emx;
Где a, b,c, m – константы.
Выбор аппроксимирующей функции не алгоритмизирован, на помощь приходит опыт составителя формулы, часто нужную аппроксимирующую функцию находят перебором. В качестве вспомогательного средства можно использовать метод выравнивания [11].
Таким образом, если вид приближающей функции установлен, то
Задача сводится к отысканию значений параметров. Их можно вычислить по методу наименьших квадратов, суть которого заключается в следующем.
Пусть требуется найти аппроксимирующую функцию, например, с тремя параметрами:
yǐ=F(xǐ,a, b,c) (1)
Для xi (где i=1,2,…,n) из таблицы эта функция примет значения ![]() I=F(xi, a,b, c), которые должны как можно меньше отличаться от заданных (табличных) значений yi, то есть разность
I=F(xi, a,b, c), которые должны как можно меньше отличаться от заданных (табличных) значений yi, то есть разность ![]() I – yi должна быть близка к нулю. Поэтому сумма квадратов разностей соответствующих значений функций F(x) и
I – yi должна быть близка к нулю. Поэтому сумма квадратов разностей соответствующих значений функций F(x) и ![]() I
I
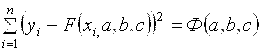
Также должна принимать минимальное значение.
Таким образом, задачу свели к отысканию минимума функции Ф(a, b,c). Используем необходимое условие экстремума:
 или
или 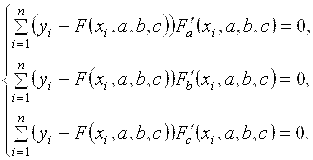 (2)
(2)
Решив эту систему из трех уравнений с тремя неизвестными, получим значения параметров a, b,c, следовательно, получим конкретный вид приближающей функции F(x, a,b, c).
Очевидно, что значения найденной функции F(x, a,b, c) в точках x1,x2,…,xn будут отличаться от табличных значений y1,y2,…,yn..
Значения разностей ![]() где i=1,2,..,n, называются отклонениями данных значений y от вычисленных по формуле (1).
где i=1,2,..,n, называются отклонениями данных значений y от вычисленных по формуле (1).
Сумма квадратов отклонений ![]() Должна быть наименьшей.
Должна быть наименьшей.
Отметим, что из нескольких приближений для одной и той же табличной функции лучшим является то, для которого ![]() имеет наименьшее значение. В нашем случае приближающая функция зависела от трех параметров, однако изменение количества параметров повлияет только на изменение количества уравнений системы (2), а суть метода останется прежней. Рассмотрим частные случаи нахождения аппроксимирующих функций.
имеет наименьшее значение. В нашем случае приближающая функция зависела от трех параметров, однако изменение количества параметров повлияет только на изменение количества уравнений системы (2), а суть метода останется прежней. Рассмотрим частные случаи нахождения аппроксимирующих функций.
Пусть требуется найти приближающую функцию в виде линейной:
F(x, a,b) = ax+b.
Так как её частные производные по параметрам a и b:![]()
![]() то система (2) примет вид:
то система (2) примет вид:

После несложных преобразований её можно привести к виду:
 (2а)
(2а)
Решив систему, получим значения параметров a и b, следовательно, и конкретный вид приближающей функции F(x, a,b) = ax+b.
Пример № 1. Найти аппроксимирующую функцию в виде линейного полинома F(x, a,b) = ax+b.
|
X |
-26 |
-22 |
-16 |
-11 |
-5 |
3 |
10 |
25 |
42 |
|
Y |
66,7 |
71,0 |
76,3 |
80,6 |
85,7 |
92,9 |
99,4 |
113,6 |
125,1 |
Составим систему уравнений, точнее, воспользуемся системой (2а). Используя имеющиеся данные, получим n = 9; ∑xi = 0; ∑yi= =811,3; ∑yi x i = 3534,8; ∑x2i = 4060. Решим систему линейных алгебраических уравнений относительно а и b, получим а = 0,87; b = 90,1.
Аппроксимирующая функция имеет вид F(x, a,b) = 0,87x+90,1.
Пусть требуется найти аппроксимирующую функцию в виде квадратичной:
F(x, a,b, c) = ax2+bx+c.
Так как её частные производные по параметрам a, b и c соответственно равны:
![]()
![]()
![]()
То система (2) примет вид:

Решив систему, получим значения параметров a, b и с, следовательно, и конкретный вид аппроксимирующей функции F(x, a,b, c)=ax2+bx+c.
| < Предыдущая | Следующая > |
|---|