3. Интерполяционная формула Лагранжа
Частным случаем задачи приближения одной функции к другой является интерполяция. Речь пойдет о приближении функции одной переменной. Задачи интерполяции возникают в практике инженера в случае:
− интерполирования табличных данных;
− получения аналитической зависимости по экспериментальным данным;
− замены сложной с вычислительной точки зрения функции более простой зависимостью;
− приближенного дифференцирования и интегрирования;
− численного решения дифференциальных уравнений.
Исходная функция у = F(x) задана на отрезке [a, b] в виде таблицы с неравноотстоящими узлами (хi+1 – хi ≠ const). Для аналитической записи этой функции с помощью интерполяционной формулы необходимо выполнение условия, состоящего в том, что исходная функция и заменяющая её функция φn(х) должны совпадать в узлах, то есть необходимо выполнение условия
F(xi) = φn(xi), где ì = 0,n. (1)
Функцию у = F(x) представим в виде полинома степени п:
Ln(х) = а0 + а 1х + а2х2 +... + апхn. (2)
Воспользуемся для этого полиномами, каждый из которых в точке х = хi (i = 0,1…) принимает значение у=1, а во всех остальных узлах x=x0,, x=x1,… , x=xi-1, x=xi+1,…, x=xn обращает y в ноль
Y=y0=y1=…=yi-1, yi+1=…=yn=0.
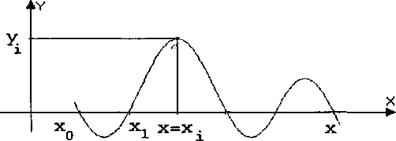
Рис. 1
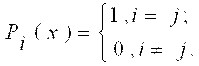
На рис. 1 изображен полином. Так как искомый полином обращается в 0 в точках, ![]() , то он имеет вид
, то он имеет вид ![]() , (3)
, (3)
Где Ci− постоянный коэффициент.
Значение этого коэффициента может быть найдено при x=xi, так как ![]() ,
,
![]() (4)
(4)
Откуда
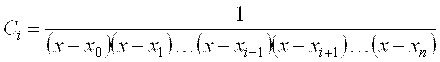 . (5)
. (5)
Подставляя (5) в (3), получим
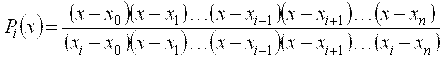 . (6)
. (6)
Степень полинома равна п. Нумерация точек начинается с 0 и заканчивается п, при этом i-я точка выпадает. Полученный полином представляет исходную функцию у = F(x) только в одной точке. Для представления всей таблично заданной функции таких полиномов потребуется п.
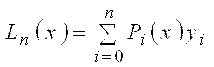 . (7)
. (7)
Рассмотрим частные случаи полинома Лагранжа при п=1; п=2; п=3.
Для п=1 исходная таблица функции будет выглядеть следующим образом:
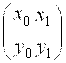 ,
,
Тогда по формуле (7) имеем
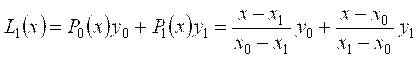 .
.
Для случая п = 2:
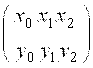 .
.

Для случая п=3:
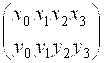 .
.
![]()


Рассмотрим конкретный пример. Функция задана таблицей своих значений. Вычислить значение функции в точке 2,5.
Значения функции y= lnx
|
Х |
2 |
3 |
4 |
5 |
|
Y= lnx |
0,6931 |
1,0986 |
1,3863 |
1,6094 |
Используем первые три значения в качестве узлов интерполирования, получим:
L2(x)=((x-3)(x-4)/(2-3)(2-4)) 0,6931+((x-2)(x-4)/(3-2)(3-4)) 1,0986+
+ ((x-2)(x-3)/(4-2)(4-3)).1,3863=-0,0589 x+0,7000 x-0,4713;
L2 (2,5)=0,9103.
Полином третьей степени строим по четырём узлам:
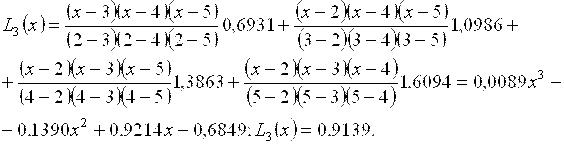
Для сравнения укажем, что в четырёхзначных таблицах значение ln2,5 = 0,9139.
Построенный полином Лагранжа совпадает с исходной функцией F(x) в узловых точках, во всех остальных точках Ln(x) представляет функцию F(x) на отрезке [a, b] приближенно. Без вывода запишем формулу, используемую для оценки погрешностей:
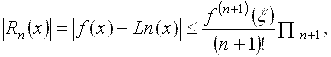 (8)
(8)
Где ![]() - остаточный член или погрешность;
- остаточный член или погрешность; ![]() - (n+1)–я производная от исходной функции, при этом будем предполагать, что F(x) на отрезке a ≤ x ≤ b изменений х будет иметь все производные до (n+1)-го порядка включительно; точка
- (n+1)–я производная от исходной функции, при этом будем предполагать, что F(x) на отрезке a ≤ x ≤ b изменений х будет иметь все производные до (n+1)-го порядка включительно; точка ![]() ,
,
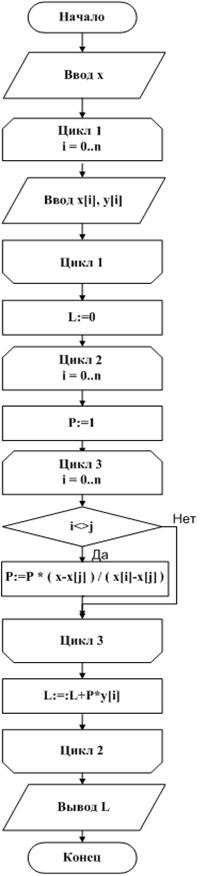
Рис. 2
Она придаёт максимальное значение функции ![]() ; n – степень
; n – степень
![]() .
.
Оценим погрешность функции, заданной таблицей, выберем степень полинома п = 2, Заданная функция y= lnx. Найдем производную третьего порядка y'=1/x; y''= –1/x2, y'''=1/x3. Очевидно, что максимальное значение y''' получим при x=2: y'''=2/23=1/4.
![]() .
.
Алгоритм выполнения задания представлен на рис. 2.
| < Предыдущая | Следующая > |
|---|