2.4. Методы решения нелинейных уравнений. Комбинированный метод хорд и касательных
Задача. Найти корень уравнения 
с заданной точностью 
.
В этом случае используется одновременно методы касательных и хорд. Приближение к корню происходит с двух сторон. Рассмотрим четыре случая, которые отвечают возможным комбинациям знаков 
и 
.
Из графиков, представленных на рис. 7, метод хорд применяется со стороны вогнутости, а метод касательных – со стороны выпуклости графика.
Совместное применение обоих методов дает сразу избыточное и недостаточное приближение. Применяя этот метод, мы предполагаем, что , и 
непрерывны на отрезке [a0, b0], причем и сохраняют свой знак. Известно, что сохранение знака у говорит о монотонности , а сохранение знака у означает, что выпуклость кривой 
при всех 
обращена в одну сторону. Для удобства расчета обозначим через а0 тот конец отрезка [a0, b0], в котором знаки 
и совпадают.
Из возможных случаев рассмотрим случай первый. Пусть 
и 
, т. е. знаки первой и второй производной совпадают. При решении уравнения каждая итерация заключается в следующем: из точки А проведем хорду, которая стягивает дугу АВ, и проведем касательную к дуге таким образом, чтобы точка пересечения касательной с осью ох оказалось внутри отрезка [a0, b0]. Хорда на графиках пересекает ось ох в точке b1,
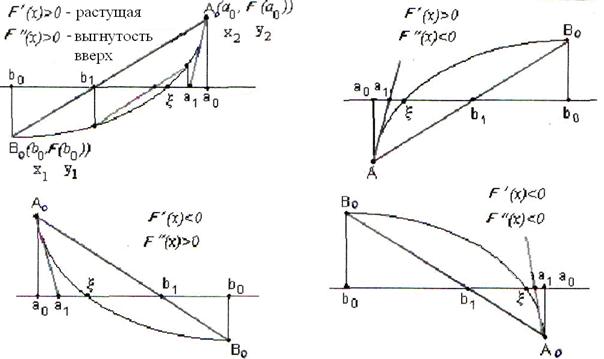
Рис. 7
Лежащей между точками b0 и искомым корнем 
, а касательная к дуге в точке А пересекает ось ох в точке а0, лежащей между точками а0 и искомым корнем уравнения 
( рис. 8).
Полученное значение a1 и b1 дают новое приближение к корню. Приведем расчетные формулы для ai+1и bi+1, выведенные в п.2.1 и 2.2.
.
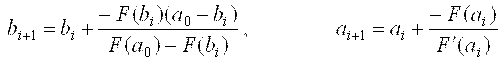Процесс нахождения ai+1 и bi+1 продолжается до тех пор, пока выполняется одно из следующих условий:
, где - 
Заданная точность;
;
.
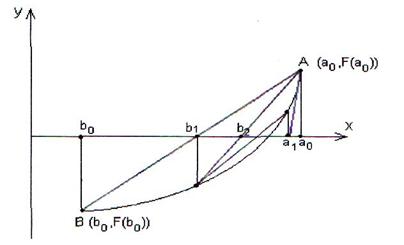
Рис. 8
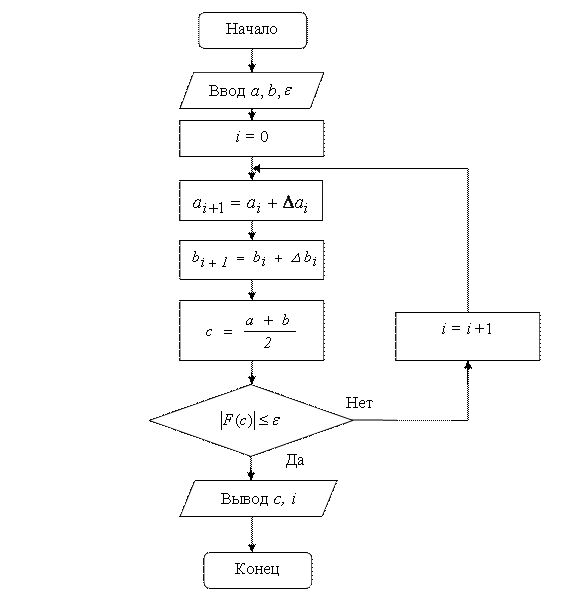
Все округления при вычислениях следует производить в сторону от корня [4]. На рис. 9 представлена блок-схема комбинированного метода хорд и касательных, где n - число итераций; аn, b n− значения приближения корня; F(аn) F(b n) − значения функции в данных точках.
2.5. Метод простой итерации (метод последовательных приближений)
Чтобы применить метод простой итерации для решения нелинейного уравнения F(x)=0, необходимо преобразовать его к следующему виду:
. (2)
Это преобразование (приведение уравнения к виду, удобному для итерации) можно выполнить различными способами; некоторые из них будут рассмотрены ниже. Функция 
называется итерационной функцией.
Выберем каким-либо образом приближенное значение корня 
и подставим его в правую часть уравнения (2). Получим значение 
. Подставим теперь 
в правую часть уравнения (2), имеем 
. Продолжая этот процесс неограниченно, получим последовательность приближений к корню, вычисляемых по формуле
. (3)
Если существует предел построенной последовательности 
, то, переходя к пределу в равенстве (3) и предполагая функцию непрерывной, получим равенство
(4)
Это значит, что 
– корень уравнения (2).
Метод допускает простую геометрическую интерпретацию. Построим графики функций у = x и у = j(x), (рис. 10,а и 10,б). Корнем x уравнения у = j(x) является абсцисса точки пересечения кривой
у = j(x) с прямой у = x. Взяв в качестве начальной произвольную точку x0 Î [a, b], строим ломаную линию. Абсциссы вершин этой ломаной представляют собой последовательные приближения корня x. Из рисунков видно, что если j'(x)<0 на отрезке [a, b], то последовательные приближения xn = j(xn-1), колеблются около корня x, если же производная j'(x)>0, то последовательные приближения сходятся к корню монотонно.
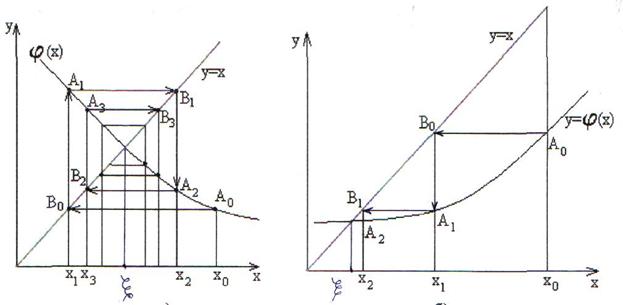
Рис. 10
При использовании метода простых итераций основным моментом является выбор функции у = j(x), эквивалентной исходной.
На рис. 11 рассмотрен пример, когда условие окончания итерационного процесса 
выполняется на первом шаге итерационного процесса, т. е. 
, из этого следует, что х0 является приближенным значением искомого корня. Однако из рис. 11 видно, что это неверно, т. к. решением задачи является x.
Для метода итераций следует подбирать функцию j(x) так, чтобы |j'(x)|£ δ <1, в противном случае процесс итерации расходящийся. При этом следует помнить, что скорость сходимости последовательности {xn} к корню x тем выше, чем меньше число δ.
Ключевой момент в применении метода простой итерации – эквивалентное преобразование уравнения F(x)=0 к виду (2). Конечно,
Рис. 11
Такое преобразование имеет смысл только тогда, когда оказывается выполненным условие 
при 
. Если первая (обычно самая простая и напрашивающаяся) попытка представления уравнения в требуемом виде оказалась неудачной, отчаиваться не следует. В ряде случаев можно использовать специальные приемы. Рассмотрим некоторые из них [2,5].
Способ 1. Если 
содержит в себе выражение некоторой обратимой на [с; d] функции 
, причем такой, что 
на [c; d], то следует попытаться заменить уравнение на равносильное с использованием обратной для функции 
: 
. Этот способ основан на известном соотношении между производными взаимообратных функций 
и следствии из него:
То 
.
Пример. Привести уравнение 
к виду, пригодному для решения методом простой итерации на интервале [0,8; 2].
Прибавим к правой и левой частям х и получим: 
. Проверим условие сходимости:
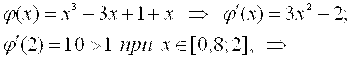
Условие сходимости не выполняется.
Другой вариант уравнения: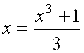 
. Проверим условие сходимости:
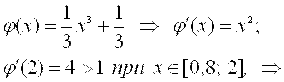
Условие сходимости не выполняется.
Так как ни одно из приведенных нами уравнений не удовлетворяет условию сходимости, то применим описанный способ:
;
Условие сходимости выполняется. Таким образом, для уточнения нужного нам корня методом простой итерации можно использовать уравнение 
.
Способ 2. В случае, когда способ 1 применить трудно или он не даст нужного результата, можно использовать следующий прием.
Пусть дано уравнение с единственным корнем в [a; b]. Предположим, что на отрезке [с; d] производная 
функции F непрерывна, не равна константе и принимает значения одного и того же знака. Будем считать, что 
, т. к. в противном случае можно рассматривать равносильное уравнение: 
.
Введем обозначения: 
.
Ясно, что 
. Заменим равносильное уравнение уравнением эквивалентным ему
И покажем, что для функции 
на [c; d] имеет место условие сходимости.
Для 
справедливы неравенства: 
. Разделим их почленно на число М и для разностей между единицей и полученными дробями получим неравенство:
,
Откуда и вытекает, что
При всех .
Пример № 1. Привести уравнение 
к виду, пригодному для решения методом простой итерации на интервале [1,4; 1,7].
Так как условие сходимости не выполняется, то применим второй способ приведения уравнения:
;
;
;
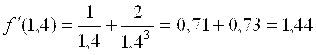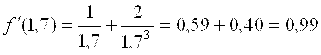Таким образом, для уточнения нужного нам корня методом простой итерации можно использовать уравнение
.
Пример № 2. Привести уравнение 
к виду, пригодному для решения методом простой итерации на интервале [1,7; 2,1].
Так как условие сходимости не выполняется, то применим второй способ приведения уравнения:
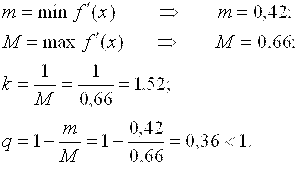
Таким образом, для уточнения нужного нам корня методом простой итерации можно использовать уравнение
.
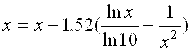Пример № 3. Привести уравнение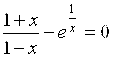 
к виду, пригодному для решения методом простой итерации на интервале [0,3;0,7].
Так как условие сходимости не выполняется, то применим второй способ приведения уравнения:
;
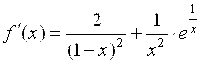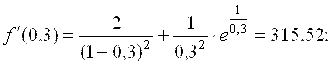
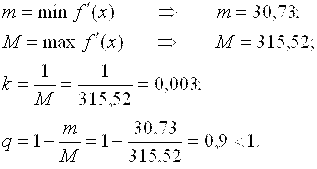
Таким образом, для уточнения нужного нам корня методом простой итерации можно использовать уравнение
.
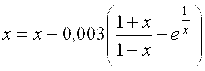Блок схема алгоритма метода простой итерации представлена на рис.12, где c – корень уравнения; n – число итераций; F(c) – значение функции в соответствующей точке.
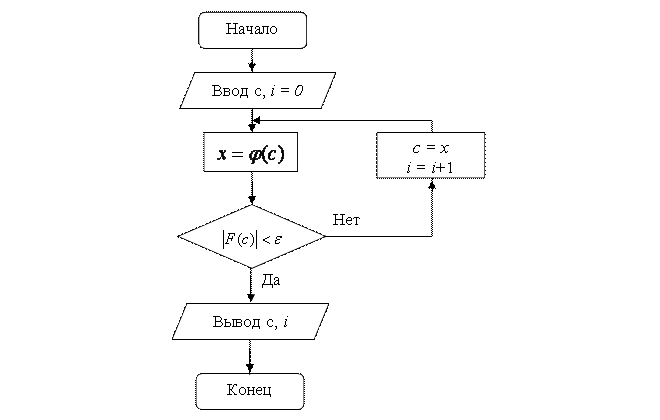
Рис. 12
| < Предыдущая | Следующая > |
|---|
