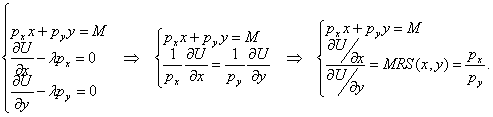15. Тема 12. Численные методы условной оптимизации

1. Рассмотрим модель поведения потребителей с функцией полезности , . Найдем оптимальные значения объемов товаров , при которых функция полезности максимальна. При этом потребитель ограничен в покупке товаров бюджетным ограничением , где — свободные денежные средства потребителя; — вектор цен за единицу товаров. В силу свойств функции полезности (см. [5, 6]) оптимальное значение потребления будет достигаться на неотрицательном значении и при выполнении равенства . Тогда задача оптимизации потребления перепишется в виде

Введем функцию Лагранжа , тогда из необходимых условий экстремума получим систему уравнений для поиска оптимальной точки :

Если функция полезности зависит только от двух видов товаров , то эта система упрощается

(12.1)

2. Пусть , капитал . Найти текущую стоимость первого товара , если его оптимальное значение равно .

Решение. Согласно пункту 1 оптимальные объемы товаров удовлетворяют системе (12.1). Найдем частные производные функции
и выпишем систему (12.1):

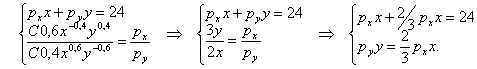
Теперь в первое уравнение подставим и найдем .

3. Пусть , , , . Найти оптимальные значение объемов потребления товаров и максимальное значение функции полезности.

Решение. Поскольку производная функции
не является непрерывной в точках , то выписать функцию Лагранжа и систему (12.1) нельзя. Воспользуемся другим определением оптимальной точки, а именно: оптимальная точка является точкой касания линии уровня (множества безразличия) и бюджетной линии.

Поскольку , то линии безразличия представляют собой лучи параллельные осям OX и OY с точками соединения . В этом случае точка касания бюджетной линии
и множества безразличия определяется из решения системы

.

4. Рассмотрим задачу оптимизации портфеля, состоящего из двух ценных бумаг. Матрица ковариаций эффективностей этих бумаг имеет вид . Найти все допустимые значения , при которых оптимальный по Марковицу портфель минимального риска содержит бумаги обоих видов. Операция «short sale» запрещена.

Решение. Задача имеет вид

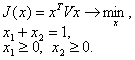
Здесь . Выразим из ограничения вторую переменную и подставим в критерий. Тогда . Поскольку переменная должна принадлежать отрезку [0; 1], то эта задача свелась к поиску минимума параболы на отрезке. Эта задача имеет решения или в точке безусловного экстремума , или в одном из концов отрезка. Для того чтобы портфель ценных бумаг содержал бумаги обоих видов, необходимо, чтобы точка попала внутрь отрезка [0; 1], т. е. должны быть выполнены неравенства . Из этих неравенств можно
найти допустимые значения .

Найдем точку из необходимого условия экстремума :

.

Из неравенства получаем, что . Из неравенства получаем, что . Пересекаем эти множества и получаем, что .

Осталось только учесть, что матрица V является ковариационной матрицей, а следовательно, должна быть неотрицательно определенной.
По критерию Сильвестра необходимо, чтобы и были неотрицательны. Из неравенства получаем, что . Окончательно .

Задачи для самостоятельного решения по теме 12

1. Пусть выпуск описывается производственной функцией Кобба-Дугласа (см. [5, 6]), где коэффициент эластичности по фондам на 50% больше коэффициента эластичности по труду. Вычислить стоимость единицы фондов, если известно, что инвестиционный капитал в 8,3(3) раза больше оптимального объема закупки фондов .

2. Пусть функция полезности имеет вид и цены , . При какой минимальной величине денежных средств может быть достигнуто значение .

3. Рассмотрим задачу оптимизации портфеля, состоящего из двух ценных бумаг. Матрица ковариаций эффективностей этих бумаг имеет вид . Найти все допустимые значения , при которых оптимальный по Марковицу портфель минимального риска содержит бумаги только
одного вида. Вычислить риск. Операция «short sale» запрещена.

4*. Рассмотрим линейную модель производства

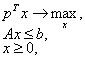
Где технологическая матрица 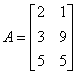, вектор ограничения по ресурсам , вектор цен , X — объемы выпускаемой продукции. Найти все допустимые значения параметра A, при которых следует производить товары обоих видов.

5**. Рассмотрим задачу оптимизации портфеля, состоящего из трех ценных бумаг

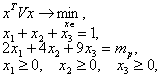
Где матрица ковариаций эффективностей ценных бумаг имеет вид . Построить аналитические зависимости оптимальных по Марковицу стратегий от неизвестного значения ожидаемой
доходности , т. е. , , . Построить графики этих зависимостей.

Указание: Значение может меняться только в пределах от 2 до 9. Для решения задачи нужно выразить из двух ограничений две переменные через третью и подставить их в критерий. Учесть положительность всех переменных. В ответе должны получиться кусочно-линейные функции.

< Предыдущая		Следующая >