16. Тема 13. Вариационное исчисление
1. Задача о наименьшей площади поверхности вращения. Среди всех плоских гладких кривых, соединяющих точки 
и 
, найти ту, которая при вращении вокруг оси абсцисс образует поверхность наименьшей площади.
Решение. Как известно, площадь вращения находится по формуле 
. Поставленная задача сводится к определению кривой 
, удовлетворяющей граничным условиям 
, 
,
на которой достигается минимум функционала 
.
Составим уравнение Эйлера (Л13.12). Подынтегральная функция
не зависит от переменной T явно (пятый случай интегрируемости, см. Л13). Поэтому уравнение Эйлера имеет первый интеграл (Л13.16):
.
После упрощения получаем 
.
Найдем общее решение дифференциального уравнения. Полагая 
, имеем 
; 
; 
.
Таким образом, искомая поверхность образуется вращением линии, уравнение которой в параметрической форме имеет вид
.
Исключая параметр 
, получаем 
— семейство цепных линий, от вращения которых образуются поверхности, называемые катеноидами.
Постоянные 
и 
находятся из граничных условий:
, 
.
В зависимости от положения точек A и B может существовать одно, два или не существовать ни одного решения.
2. Найти экстремаль функционала
,
Удовлетворяющую граничным условиям 
, 
.
Решение. Запишем уравнение Эйлера. Так как 
, 
, 
, 
, то получаем 
или 
.
Найдем общее решение уравнения Эйлера. Оно является линейным
с постоянными коэффициентами, поэтому составим характеристическое уравнение 
. Его корни 
, 
— действительные, разные числа. Общее решение уравнения имеет вид
.
Определим коэффициенты и из граничных условий:
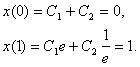
Отсюда 
. В результате получаем экстремаль 
.
3. Найти экстремум функционала
.
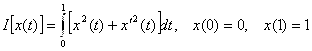Решение. Экстремаль для этого функционала найдена в задаче 2: . Проверим достаточные условия сильного экстремума.
Для проверки условия Якоби составим уравнение Якоби (Л13.17). Так как , 
, 
, 
, то уравнение имеет вид 
. Отсюда 
и 
— общее решение этого линейного дифференциального уравнения. Из условия 
получаем 
и 
. Так как нетривиальное решение (при 
) уравнения Якоби не равно нулю, т. е. 
при 
, то условие Якоби выполняется.
Так как функция 
трижды дифференцируема по 
,
то применим условие Лежандра. Поскольку 
при любых ,
то на кривой 
достигается сильный минимум. Очевидно, что на этой же кривой достигается и слабый минимум.
Задачи для самостоятельного решения по теме 13
1. Найти экстремаль функционала
,
Удовлетворяющую граничным условиям 
, .
2*. Найти экстремум функционала
| < Предыдущая |
|---|
