14. Тема 11. Численные методы безусловной оптимизации

1. Рассмотрим задачу Марковица построения оптимального инвестиционного портфеля ценных бумаг. Математическая формулировка задачи имеет вид:

.

(11.1)

Здесь (Xi,…,Xn)T, где N — количество ценных бумаг; Xi — доля
капитала, инвестированного в бумаги I-го типа; — доля капитала, вложенная в безрисковую ценную бумагу с доходностью ; , где — доходность I–ой бумаги; , где — риск портфеля; — ожидаемая доходность портфеля; — ковариационная матрица эффективностей ценных бумаг; . Матрица V и вектор M считаются известными.

Поскольку задача (11.1) является многокритериальной, то поступают следующим образом: фиксируют значение квадрата риска или ожидаемую доходность и решают полученную задачу оптимизации.

Решим задачу (11.1) при фиксированном значении .

Решение. Задача имеет вид:

.

(11.2)

Поскольку задача содержит ограничения только в виде равенств,
с помощью функции Лагранжа (Л12.4) приведем эту задачу к задаче без ограничений. Так как градиенты ограничений задачи линейно независимы, то . Выпишем функцию Лагранжа:

.

Тогда из необходимых условий экстремума (Л12.6) имеем:

.

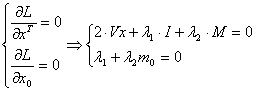Выражая из второго уравнения , получим . Подставим его в первое уравнение, тогда . Следовательно,

.

(11.3)

Исключая из ограничений, получим . Подставим сюда выражение (11.3):

.

Обозначим , тогда, подставляя в (11.3), получим

.

Вычислим риск :

.

Из этого равенства следует, что риск оптимального портфеля зависит от линейно.

2. Методами градиентного и покоординатного спуска с постоянными шагами найти локальный минимум функции .

Решение. Будем продолжать итерационные процедуры до тех пор,
пока не будут выполнены два неравенства

,

Где K — номер итерации, а точность .

Условия сходимости алгоритмов для этой функции выполнены
(см. теоремы 3 и 4 из Л11). Сначала найдем точку методом градиентного спуска с постоянным шагом [см. Л11 и формулу (Л11.8)].

0. Пусть , . Градиент функции .

1. Вычислим . Зададим начальный шаг .

Вычислим ; .

Сравним с . Имеем . Вывод: условие не выполнено, нужно уменьшить шаг. Зададим
и повторим первую итерацию.

Вычислим ; .

Сравним с . Имеем . Вывод: увеличим K на 1
и перейдем ко второй итерации.

2. Проверим выполнение условий окончания

.

Эти условия не выполнены – значит, ищем следующую точку.

Вычислим . Зададим начальный шаг .

Вычислим ; .

Сравним с . Вывод: , переходим к следующей итерации.

3. Проверим выполнение условий окончания

.

Эти условия одновременно не выполнены – значит, ищем следующую точку.

Вычислим . Зададим начальный шаг .

Вычислим ; .

Сравним с . Вывод: , переходим к следующей итерации.

4. Проверим выполнение условий окончания

.

Эти условия выполнены, расчет окончен.

Проверим выполнение достаточных условий минимума в этой точке. Функция является дважды непрерывно дифференцируемой, поэтому вычислим матрицу Гессе . Матрица постоянна и по критерию Сильвестра является положительно определенной. Следовательно, точка есть приближение к локальному минимуму ,
а есть приближенное значение для .

Теперь найдем приближение методом покоординатного спуска.
В методе покоординатного спуска на каждой итерации меняется последовательно одна из координат переменной X (см. Л11). В нашем случае это и .

0. Пусть , . Градиент функции .

1. Зададим и найдем новую точку, изменяя первую координату.

Вычислим 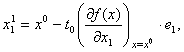где 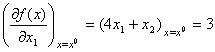, . Отсюда , .

Сравним с . Вывод: , значит, полагаем и выполняем вычисления заново.

Получаем, что , .

Сравним с . Вывод: , меняем вторую координату.

Вычислим где , . Отсюда , .

Сравним с . Вывод: , переходим ко второй итерации.

2. Проверим выполнение условий окончания

.

Эти условия не выполнены – значит, ищем следующую точку.

Полагаем , .

Вычислим

Сравним с . Вывод: , меняем вторую координату.

Вычислим .

Сравним с . Вывод: , переходим к следующей итерации.

3. Проверим выполнение условий окончания

.

Условия окончания выполнены. Окончательно полагаем .

Эта точка является приближением к , а есть приближенное значение для .

Задачи для самостоятельного решения по теме 11

1*. Решить задачу (11.1) при фиксированном значении .

2. Методами градиентного и покоординатного спуска с постоянными шагами найти локальный минимум функции .
Сделать не более пяти итераций, если точность не будет достигнута.

< Предыдущая		Следующая >
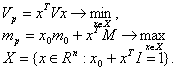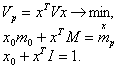