13. Тема 10. Задача оптимизации

1. Для функции вычислить градиент и матрицу Гессе в точках , .

Решение. По определению градиента и матрицы Гессе (см. Л11) имеем:

, ,

,

,

,.

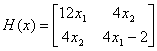2. Исследовать выпуклость функции на множестве .

Решение. Если матрица Гессе , то функция является
выпуклой. Вычислим матрицу Гессе: . По критерию Сильвестра исследуем матрицу . Для этого вычислим угловые миноры матрицы , . Поскольку оба минора больше нуля,
матрица Гессе будет положительно определенной, а функция
выпуклой.

3. Проверить условие Липшица (см. теорему 3 из Л11) для функции на отрезке .

Решение. Условие Липшица имеет вид . Если функция имеет непрерывную производную, то константа Липшица задается равенством . В нашем случае константа Липшица , следовательно, .

Задачи для самостоятельного решения по теме 10

1. Для функции вычислить градиент и матрицу Гессе в точках , .

2. Исследовать выпуклость функции на множестве .

3. Проверить условие Липшица для функции на отрезке .

< Предыдущая		Следующая >