12. Тема 9. Численное решение обыкновенных дифференциальных уравнений

Пусть известно, что производственная функция является
линейно однородной, а предельная норма замещения труда фондами , где K — фондовооруженность. Кроме того, в точке
и равна 2. Найти значение валового выпуска в точке .

Решение. Чтобы решить задачу, нужно найти выражение для функции . Поскольку является линейно однородной, то для нее зависит только от фондовооруженности (см. [5]) , а именно , где функция задается уравнением .
Теперь для решения задачи достаточно определить из дифференциального уравнения с начальным условием .
Это уравнение можно решить аналитически и получить функцию , после этого вычислить . Мы решим это уравнение численно с помощью метода Эйлера (см. Л9) на отрезке с начальным условием и шагом .

Преобразуем исходное уравнение к виду:

.

Основная формула метода Эйлера (Л9.12) в нашем случае имеет вид:

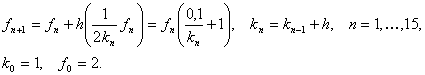
Результаты вычислений представим в табл. 11 вместе с точными значениями, полученными из аналитического решения уравнения.

Таблица 11

N
0	1	2	2
2	1,4	2,383	2,366
4	1,8	2.712	2,683
5	2	2,863	2,824
7	2,4	3,142	3,098
9	2,8	3,399	3,347
10	3	3,520	3,464
12	3,4	3,741	3,688
14	3,8	3,958	3,899
15	4	4,062	4

Вычислим приближенное значение валового выпуска . Видно, что решение методом Эйлера дает завышенное значение, но достаточно точное.

Задачи для самостоятельного решения по теме 9

1. Пусть — линейно однородная производственная функция
с предельной нормой замещения труда фондами . Кроме того, в точке и равна . Найти значение валового выпуска в точке .

Указание: Дифференциальное уравнение решить аналитически
и методом Эйлера с шагом .

< Предыдущая		Следующая >