11. Тема 8. Метод статистических испытаний
Вычислить методом Монте-Карло интеграл
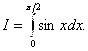
Точное значение этого интеграла равно 
. Используем для вычисления интеграла две различные случайные величины 
: с постоянной плотностью 
(т. е. равномерно распределена в интервале 
) и с линейной плотностью 
. Линейная плотность лучше соответствует рекомендации о том, что желательна пропорциональность 
и 
(см. тему 8 плана-конспекта лекционного курса). Поэтому можно ожидать, что второй способ вычисления даст лучший результат.
1. 
. Формула для вычисления интеграла имеет вид
Пусть 
. Смоделируем десять реализаций равномерной СВ
на отрезке . Для этого нужно взять реализации равномерной СВ
на отрезке [0,1] и умножить их на величину 
. Промежуточные результаты сведены в табл. 9. Результат расчета: 
.
Таблица 9
|
J |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
1,359 |
0,250 |
0,124 |
0,889 |
0,243 |
1,043 |
0,542 |
1,029 |
1,275 |
0,521 |
|
|
0,978 |
0,247 |
0,124 |
0,776 |
0,241 |
0,864 |
0,516 |
0,857 |
0,957 |
1,498 |
2. 
. Для разыгрывания используем формулу (Л8.1)
из конспекта:
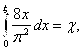
Откуда после несложных вычислений получим
Формула для вычисления интеграла принимает вид
Пусть . Смоделируем десять реализаций равномерной СВ
. Промежуточные результаты сведены в табл. 10. Результат расчета: 
.
Таблица 10
|
J |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0,865 |
0,159 |
0,079 |
0,566 |
0,155 |
0,664 |
0,345 |
0,655 |
0,812 |
0,332 |
|
|
1,461 |
0,626 |
0,442 |
1,182 |
0,618 |
1,280 |
0,923 |
1,271 |
1,415 |
0,905 |
|
|
0,680 |
0,936 |
0,968 |
0,783 |
0,937 |
0,748 |
0,863 |
0,751 |
0,698 |
0,868 |
Как и предполагалось, второй способ вычисления дал более точный результат.
По значениям, приведенным в таблицах, можно приближенно вычислить дисперсии 
для обоих случаев расчета (см. [Л8.8]). Для метода 1
Для метода 2
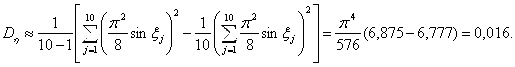
Несмотря на то, что значение невелико и приближенная
нормальность оценки (Л8.7) из конспекта не гарантирована, вычислим
для обоих методов величины 
для 
. Получим значения 0,103 и 0,027. Видно, что фактические абсолютные погрешности при расчете интеграла, равные 0,048 и 0,016 (получены вычитанием точного значения интеграла и приближенного значения), — величины того же порядка. Заметим, что точные значения в рассмотренном примере равны 0,233
и 0,0166. Таким образом, и при оценке дисперсий второй метод оказался точнее первого.
Задачи для самостоятельного решения по теме 8
1*. Вычислить методом Монте-Карло интеграл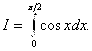 
| < Предыдущая | Следующая > |
|---|
