09. Тема 6. Численное дифференцирование
Найти значение предельной нормы замещения труда фондами ![]()
в точке ![]() и
и ![]() , если для различных значений K и L мы можем
, если для различных значений K и L мы можем
наблюдать значение валового выпуска ![]() , где F – некоторая неизвестная производственная функция.
, где F – некоторая неизвестная производственная функция.
Решение. Поскольку 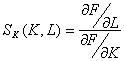 (см. [5 ,6]), то нам требуется
(см. [5 ,6]), то нам требуется
построить приближенное значение частных производных в точке ![]() . Для нахождения этих значений воспользуемся формулой численного дифференцирования (Л6.2) на некотором отрезке. Эта формула дает наименьшую погрешность в середине отрезка, на котором строится аппроксимация производной. Поэтому будем строить аппроксимацию
. Для нахождения этих значений воспользуемся формулой численного дифференцирования (Л6.2) на некотором отрезке. Эта формула дает наименьшую погрешность в середине отрезка, на котором строится аппроксимация производной. Поэтому будем строить аппроксимацию
частных производных на отрезке ![]() с центром в точке 2. Вычислим требуемые значения валового выпуска X, считая другую переменную равной двум:
с центром в точке 2. Вычислим требуемые значения валового выпуска X, считая другую переменную равной двум:
|
(1, 2) (2, 2) (4, 2)
6,964 8 8,676 |
(2, 1) (2, 2) (2, 4)
4,595 8 11,065 |
Теперь по формуле (Л6.1) вычисляем производные на отрезке ![]() :
:
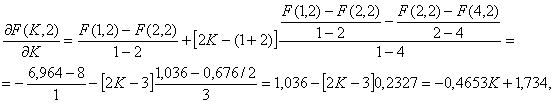
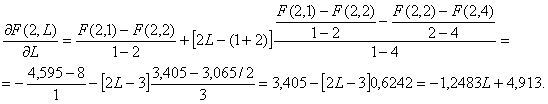
Приближенное значение ![]() равно
равно 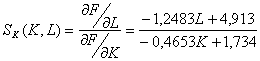 для
для ![]() и
и ![]() . Тогда значение в точке (2, 2) равно
. Тогда значение в точке (2, 2) равно ![]() .
.
Для сравнения приведем точное значение ![]() . Значения в таблице были вычислены для производственной функции Кобба-Дугласа
. Значения в таблице были вычислены для производственной функции Кобба-Дугласа ![]() (см. [5 ,6]). Для нее
(см. [5 ,6]). Для нее
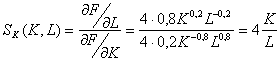 ;
; ![]() .
.
Отсюда видно, что аппроксимация частной производной по переменной L оказалась недостаточно точной, и значения ![]() различаются на единицу.
различаются на единицу.
Задачи для самостоятельного решения по теме 6
1. Найти приближенное значение предельной нормы замещения труда фондами ![]() в точке
в точке ![]() и
и ![]() . Значение валового выпуска X вычислить для функции
. Значение валового выпуска X вычислить для функции ![]() в трех точках K и L, равных
в трех точках K и L, равных ![]() . Сравнить приближенное значение с точным.
. Сравнить приближенное значение с точным.
| < Предыдущая | Следующая > |
|---|