07. Тема 4. Приближение функций

Рассмотрим производственную функцию . Если зафиксировать значение трудового показателя L равным 4 и для разных значений капитала определить валовой выпуск, то получатся значения ; ; . По этим значениям требуется построить приближенную производственную функцию. Для построения такой функции можно воспользоваться интерполяционными многочленами в форме Лагранжа и Ньютона, сплайнами и методом наименьших квадратов (см. тему 4 лекций). Для удобства изложения обозначим через , тогда при , , функция равна: , , .

1. По формуле (Л4.6) построим многочлен Лагранжа второй степени на :

2. По формуле (Л4.10) построим многочлен Ньютона второй степени на :

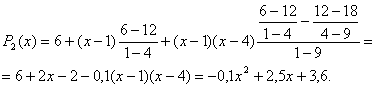
Заметим, что , как и должно быть согласно утверждению 1 из Л4. Для проверки правильности построения многочленов можно посчитать значения в точках , которые должны быть равны значениям функции. В нашем случае это выполнено: ; ; .

3. Оценим погрешность интерполяции. Для этого нужно знать истинную функцию . На практике эта функция неизвестна,
но в учебных целях оценить погрешность нужно. В нашем случае значения были взяты для функции . Тогда по формулам (Л4.12)–(Л4.13) для получим

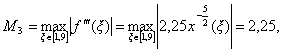
Т. е. максимум третьей производной функции достигается в точке , поскольку функция является монотонно убывающей на отрезке [1; 9]. Теперь можно оценить погрешность интерполяции:

Оценим погрешность в точках и : ; .

4. Построим два сплайна второго порядка на отрезках и . Для этого надо решить систему уравнений для шести параметров:

В нашем случае , тогда , , , , и из последних двух уравнений получаем:

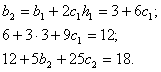
Решая эти уравнения, находим: , , . Теперь, подставляя эти параметры в выражение , получим два сплайна для двух отрезков [1; 4] и [4; 9].

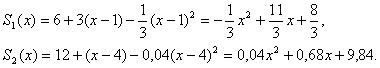
Для сплайнов тоже можно сделать проверку: , , , .

5. Построим методом наименьших квадратов прямую линию по трем значениям, т. е. . Для этого нужно посчитать матрицу W и вектор V (см. Л4):

Теперь, решая систему нормальных уравнений , получим уравнение . Как видно из уравнения, эта прямая линия не проходит через исходные точки в отличие от интерполяционных многочленов и сплайнов.

Задачи для самостоятельного решения по теме 4

1. Для функции и значений , ,
построить интерполяционные многочлены в форме Лагранжа и Ньютона, оценить погрешность интерполяции, построить два сплайна второго
порядка и методом наименьших квадратов провести прямую линию.

< Предыдущая		Следующая >