1.6. Принцип стискуючих відображень
Ряд питань, пов’язаних із існуванням і єдиністю розв’язків рівнянь того чи іншого типу (наприклад, диференціальних), можна сформулювати як існування нерухомої точки при деякому відображенні існуючого метричного простору самого в себе. Серед різних критеріїв існування і єдиності нерухомої точки одним із найпростіших і одночасно найважливіших є принцип стиску-ючих відображень.
Нехай ![]() – метричний простір із відстанню
– метричний простір із відстанню ![]() . Відображення
. Відображення ![]() називається Стискуючим або Стисканням, якщо існує таке додатне число
називається Стискуючим або Стисканням, якщо існує таке додатне число ![]() , що для будь-яких
, що для будь-яких ![]() виконується нерівність
виконується нерівність
![]() (1.6)
(1.6)
Очевидно, що будь-яке стискуюче відображення неперервне. Дійсно, якщо ![]() , то згідно нерівності (1.6)
, то згідно нерівності (1.6) ![]() .
.
Точка ![]() називається Нерухомою точкою відображення
називається Нерухомою точкою відображення ![]() , якщо
, якщо ![]() , тобто нерухома точка є розв’язком рівняння
, тобто нерухома точка є розв’язком рівняння ![]() .
.
Теорема 1.6. (Принцип стискуючих відображень). Будь-яке стискуюче відображення ![]() , яке діє в повному метричному просторі
, яке діє в повному метричному просторі ![]() , має одну й тільки одну нерухому точку.
, має одну й тільки одну нерухому точку.
Доведення. Нехай ![]() – довільна точка. Припустимо, що
– довільна точка. Припустимо, що ![]() ,
, ![]() , …,
, …, ![]() . Послідовність
. Послідовність ![]() є фундаменталь-ною. Дійсно, взявши для однозначності
є фундаменталь-ною. Дійсно, взявши для однозначності ![]() , маємо
, маємо
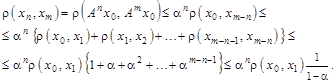
Оскільки ![]() , то при досить великих значеннях
, то при досить великих значеннях ![]() ця величина є як завгодно малою. В силу повноти
ця величина є як завгодно малою. В силу повноти ![]() послідовність
послідовність ![]() має границю. При-пустимо, що
має границю. При-пустимо, що ![]() . В силу неперервності
. В силу неперервності ![]() маємо
маємо
![]() .
.
Таким чином нерухома точка існує. Доведемо її єдиність.
Якщо![]() ,
, ![]() , то з нерівності (1.6) витікає
, то з нерівності (1.6) витікає
![]() .
.
Оскільки ![]() , то звідси випливає, що
, то звідси випливає, що ![]() , тобто
, тобто ![]() .
.
Застосуємо теорему 1.6 для доведення теореми існування і єдиності роз-в’язку диференціального рівняння.
Розглянемо диференціальне рівняння
![]() (1.7)
(1.7)
З початковою умовою ![]() . Нехай
. Нехай ![]() визначена і неперервна в деякій області
визначена і неперервна в деякій області ![]() , яка містить точку
, яка містить точку ![]() і задовольняє в цій області умові Ліпшиця по Y:
і задовольняє в цій області умові Ліпшиця по Y:
![]() .
.
Нехай ![]() таке число, що
таке число, що ![]() . Покажемо, що на відрізку
. Покажемо, що на відрізку ![]() існує й до того ж тільки один розв’язок рівняння (1.7).
існує й до того ж тільки один розв’язок рівняння (1.7).
Рівняння (1.7) разом з початковими умовами є еквівалентним інтеграль-ному рівнянню
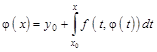 . (1.8)
. (1.8)
В силу неперервності ![]() маємо оцінку
маємо оцінку ![]() в деякій області
в деякій області ![]() , яка містить точку
, яка містить точку ![]() . Підберемо
. Підберемо ![]() так, щоб
так, щоб ![]() , якщо
, якщо ![]() і
і ![]() .
.
Позначимо через ![]() простір неперервних функцій
простір неперервних функцій ![]() , визначених на
, визначених на ![]() і таких, що
і таких, що ![]() з метрикою
з метрикою
![]() .
.
Простір ![]() – повний, оскільки він є замкненою підмножиною простору
– повний, оскільки він є замкненою підмножиною простору ![]()
![]() .
.
Розглянемо відображення ![]() , визначене формулою
, визначене формулою
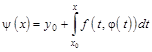 ,
,
Де ![]() . Покажемо, що
. Покажемо, що ![]() . Дійсно, для будь-якого
. Дійсно, для будь-якого ![]()
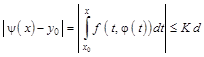 ,
,
Тобто ![]() . Крім того
. Крім того
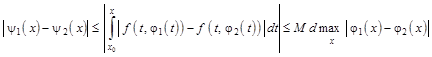 .
.
Оскільки ![]() , то
, то ![]() – оператор стискання. Звідси витікає існування й єдиність такого
– оператор стискання. Звідси витікає існування й єдиність такого ![]() , що
, що ![]() , тобто виконується рівняння (1.8).
, тобто виконується рівняння (1.8).
| < Предыдущая | Следующая > |
|---|