1.2. Приклади

Приклад 1.1. Для довільного Припустимо

Такий простірМожна назвати простором ізольованих точок.

Приклад 1.2. Множина дійсних чисел з відстанню утворює метричний простір.

Приклад 1.3. Множина -вимірних векторів з від-станню

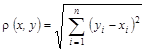(1.1)

Називається -вимірним арифметичним евклідовим простором . Справед-ливість аксіом 1) і 2) для очевидна. Покажемо, що виконується умова 3). Нехай , , – деякі точки з . Тоді з (1.1) витікає, що аксіома 3) має вигляд

. (1.2)

Припустимо , , тоді і нерівність (1.2) матиме вигляд

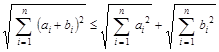. (1.3)

Для доведення (1.3) використовують нерівність Коші-Буняковського

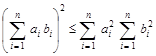. (1.4)

Нерівність (1.4) безпосередньо витікає з тотожності

,

Яка перевіряється безпосередньо.

З урахуванням нерівності (1.4) одержуємо:

.

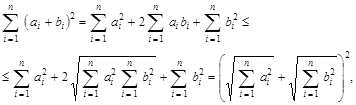Що доводить справедливість нерівності (1.3).

Приклад 1.4. Розглянемо ту саму множину векторів , але
з відстанню

.

Такий метричний простір позначимо .

Приклад 1.5. Розглянемо ту саму множину, що й у прикладах 1.3, 1.4, але з відстанню . Такий метричний простір позначимо .

Очевидно, що простір Є в деякому розумінні проміжним простором між просторами і . Виявляється, що існує ціла сім’я таких проміжних просторів.

Приклад 1.6. Розглянемо ту саму множину, що й у прикладах 1.3–1.5. За відстань оберемо функцію

,

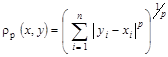Де . Такий простір позначимо .

Із визначення витікає, що . З іншого боку можна показати, що

.

Приклади 1.4–1.6 показують, що в просторі векторів можна ввести багато різних метрик, а не тільки одну евклідову.

В прикладах 1.2–1.6 наведено досить добре вивчені скінченномірні прос-тори. Перейдемо до розгляду більш складних нескінченномірних просторів.

Приклад 1.7. Через позначається простір всіх послідовностей дійсних чисел таких, що

,

А відстань визначається формулою

.

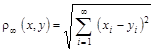Із очевидної нерівності витікає, що така функція визначена для всіх . Аксіоми 1), 2) тривіальні, а аксіома 3) доводиться граничним переходом із формули (1.3).

Приклад 1.8. Узагальнимо приклад 1.6. Через позначається множина послідовностей таких, що

,

А відстань визначається за формулою

.

Тут .

Зазначимо, що якщо раніше в прикладах 1.3–1.6 множини елементів у метричних просторах співпадали, то в прикладі 1.8 це не так, тобто , якщо . Наприклад, послідовність , але .

Приклад 1.9. Розглянемо множину всіх обмежених послідовностей і припустимо

.

Такий простір позначається через або .

Перейдемо до розгляду просторів функцій.

Приклад 1.10. Через позначається простір всіх неперервних функцій, визначених на інтервалі з відстанню

.

Такий простір називають простором з рівномірною метрикою.

Приклад 1.11. Через позначається простір всіх неперервних диференційованих функцій, визначених на з відстанню

.

Приклад 1.12. Розглянемо множину всіх неперервних функцій, визна-чених на , з відстанню

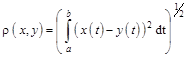. (1.5)

Такий простір називається простором з квадратичною метрикою. Однак, як буде видно в подальшому, цей простір не володіє багатьма властивостями. Тому розглянемо ширші простори.

Приклад 1.13. Через позначимо множину всіх вимірних функцій , таких, що

З відстанню, заданою формулою (1.5).

Більш узагальнений випадок наступний.

Приклад 1.14. Через позначимо множину всіх вимірних функ-цій таких, що

З відстанню

,

Де . Відзначимо, що , якщо .

1.3. Неперервні відображення
метричних просторів

Нехай і – два метричних простори з метриками і ; – відоб-раження в .

Визначення 1.2. Відображення називається неперервним у точці , якщо для будь-якого існує таке , що для всіх таких, що виконується нерівність .

Якщо неперервна в усіх точках , то кажуть, що непе-рервна на .

Якщо і – числові множини, наприклад, , то маємо зви-чайне визначення неперервності з курсу математичного аналізу.

Якщо відображення : взаємно однозначне, то існує обернене відображення простору на простір . Якщо і непе-рервні, то називається гомеоморфізмом або гомеоморфним відображенням простору на простір .

Якщо існує гомеоморфізм :, то кажуть, що простори і гомеоморфні.

Приклад 1.15. Числова пряма гомеоморфна інтервалу . Гомеоморфізм визначається формулою

.

Важливим частинним випадком гомеоморфізму є такий, що зберігає метрику. Кажуть, що бієкція між метричними просторами і є ізомет-рією, якщо

Для всіх . При цьому простори і називаються ізометричними.

Слід зауважити, що у прикладі 1.15 простори неізометричні між собою.

< Предыдущая		Следующая >