5. Методические указания к выполнению контрольной работы

Задание на контрольную работу

В контрольной работе студенту предлагается выполнить четыре задания, номера задач нужно выбрать в соответствии с последней и предпоследней цифрами шифра, а также первой буквой фамилии из таблицы, приведенной ниже.

Посл. цифра шифра	1	2	3	4	5	6	7	8	9	0
№.задач	1	2	3	4	5	6	7	8	9	10
Предпосл. цифра шифра	1	2	3	4	5	6	7	8	9	0
№ задач	11	12	13	14	15	16	17	18	19	20
Первая буква фамилии	А, И,Т	Б, О,Ц	В, М	Г, Ф. Ч	Д, З Л, Х	Е, Н	Ж, С, Р	К, Э	П, Щ	У, Ш, Ю, Я
№ задач	30	29	28	27	26	25	24	23	22	21

Задание 1

1. Бросаются три игральных кубика. Найти вероятности событий:

А – на всех кубиках одинаковое число очков;

B – на всех кубиках выпало в сумме три очка;

С – на всех кубиках выпало в сумме более трех очков.

2. Бросаются три игральных кубика. Найти вероятности событий:

А – на всех кубиках в сумме выпало ровно четыре очка;

B – на всех кубиках в сумме выпало не менее четырех очков;

С – на всех кубиках в сумме выпало более четырех очков.

3. Бросаются три игральных кубика. Найти вероятности событий:

А – на всех кубиках разное число очков;

B – на всех кубиках выпало в сумме восемнадцать очков;

С – на всех кубиках выпало в сумме менее восемнадцати очков.

4. В каждой из трех коробок находится по три белых и пять красных шаров. Из каждой коробки наудачу вынимается по одному шару. Найти вероятности событий:

А – все шары белые;

В – только один шар белый;

С – хотя бы один шар белый.

5. В каждой из трех коробок находится по три белых и пять красных шаров. Из каждой коробки наудачу вынимается по одному шару. Найти вероятности событий:

А – все шары красные;

В – только один шар красный;

С – хотя бы один шар красный.

6. На сборку поступило десять деталей, среди которых четыре бракованные. Сборщик наудачу берет три детали. Найти вероятности событий:

А – все взятые детали стандартные;

В – только одна деталь среди взятых стандартная;

С – хотя бы одна из взятых деталей стандартная.

7. На сборку поступило десять деталей, среди которых четыре бракованные. Сборщик наудачу берет три детали. Найти вероятности событий:

А – все взятые детали бракованные;

В – только одна деталь среди взятых бракованная;

С – хотя бы одна из взятых деталей бракованная.

8. В группе спортсменов два мастера спорта, шесть кандидатов в мастера и восемь перворазрядников. По жребию выбирается четыре спортсмена. Найти вероятности событий:

А – все четыре выбранные спортсмена оказались перворазрядниками;

В – среди выбранных спортсменов хотя бы один оказался перворазрядником;

С – среди выбранных спортсменов ровно половина оказалась перворазрядниками.

9. В группе спортсменов два мастера спорта, шесть кандидатов в мастера и восемь перворазрядников. По жребию выбирается четыре спортсмена. Найти вероятности событий:

А – все четыре выбранные спортсмена оказались кандидатами в мастера спорта;

В – среди выбранных спортсменов хотя бы один оказался кандидатом в мастера спорта;

С – среди выбранных спортсменов оказалось два мастера спорта и два кандидата в мастера спорта.

10. В группе спортсменов два мастера спорта, шесть кандидатов в мастера и восемь перворазрядников. По жребию выбирается четыре спортсмена. Найти вероятности событий:

А – среди выбранных спортсменов оказались два мастера спорта;

В – среди выбранных спортсменов хотя бы один оказался мастером спорта;

С – среди выбранных спортсменов оказались один мастер спорта, один кандидат в мастера спорта и два перворазрядника.

Задание 2

11. Известна плотность вероятности случайной величины

.

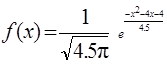Найти её математическое ожидание, дисперсию; построить кривую вероятности; найти вероятности событий: А – случайная величина примет только положительные значения, В – случайная величина попадает в интервал, симметричный относительно математического ожидания, длиной два средних квадратических отклонения.

12. Случайная величина распределена по нормальному закону; среднее квадратическое отклонение её равно 5 , P{X<3}=0.2. Найти математическое ожидание, дисперсию; построить кривую вероятности; найти вероятность события: А – случайная величина попадает в интервал (M+s; M+2s).

13. Случайная величина распределена по нормальному закону с математическим ожиданием m=-3. P{X>3}=0.15. Найти её дисперсию; построить кривую вероятности; вычислить вероятность отрицательных значений случайной величины.

14. Плотность вероятности случайной величины

.

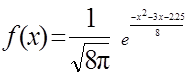Найти математическое ожидание случайной величины, её дисперсию; построить кривую вероятности; найти вероятности событий: А – случайная величина примет значение меньше 1, В – случайная величина примет значение больше ( –2).

15. Случайная величина распределена по нормальному закону с математическим ожиданием 5 и вероятностью попадания в интервал (7;¥) равной 0,4. Найти её дисперсию; построить кривую вероятности; вычислить вероятность попадания в интервал (M-s; M+s).

16. Случайная величина распределена по нормальному закону с s = 8, вероятность попадания в интервал (-¥;4) равна 0,3. Найти её математическое ожидание, дисперсию; построить кривую вероятности; вычислить вероятности событий: А – случайная величина принимает положительные значения, В – случайная величина попадает в интервал, симметричный относительно математического ожидания, длиной четыре средних квадратических отклонения.

17. Плотность вероятности случайной величины

.

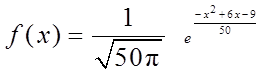Найти её математическое ожидание, дисперсию; построить кривую вероятности; найти интервал, симметричный относительно математического ожидания, вероятность попадания в который равна 0,8.

18. Случайная величина распределена по нормальному закону со средним квадратическим отклонением s = 5 и вероятностью принять значение больше 10 равной 0,4. Найти её математическое ожидание, дисперсию; построить кривую вероятности; найти вероятность попадания случайной величины в интервал (-2;8).

19. Математическое ожидание случайной величины, распределенной по нормальному закону, равно –2, а вероятность попасть в интервал |h + 2| < 4 равна 0,4. Найти её дисперсию; построить кривую вероятности; вычислить вероятности событий : А – случайная величина примет значение больше M + s, В – случайная величина примет отрицательные значения.

20. Плотность вероятности случайной величины

.

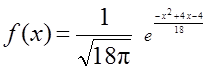Найти её математическое ожидание, дисперсию, построить кривую вероятности; найти вероятности событий: А – случайная величина примет только отрицательные значения, В – случайная величина попадает в интервал, симметричный относительно математического ожидания, длиной три средних квадратических отклонения.

Задание 3

В заданиях 21 – 30 рассматривается прибор, состоящий из двух независимо работающих блоков А и В, каждый из которых состоит из нескольких элементов. Известны вероятности отказов каждого из элементов: P1=0.3, P2=0.2, P3=0.1, P4=0.1, P5=0.2, P6=0.2, P7=0.3. При отказе блока он подлежит полной замене, причем стоимость замены блока А составляет С1, блока В – С2 Единиц стоимости. Предполагается, что за период времени Т замененный блок не выйдет ещё раз из строя.

1. Найти случайную величину h – стоимость восстановления прибора за период времени Т:

1.1. построить её ряд и функцию распределения;

1.2. вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение.

2. Построить модель найденной случайной величины для двадцати приборов (методом жребия получить её 20 значений):

2.1. найти экспериментальные ряд и функцию распределения;

2.2. найти оценки математического ожидания, дисперсии и среднего квадратического отклонения;

2.3. построить графики теоретического и экспериментального ряда и функции распределения.

3. С помощью критерия Пирсона оценить соответствие экспериментального распределения теоретическому при уровне значимости a = 0,05.

Замечание. Расчеты произвести с точностью до четырех знаков после запятой.

Варианты схем для задания 3 указано в прилагаемом отдельно файле Контрольная УМК Ход. Doc.

Задание 4

В четвертом задании предполагается, что случайная величина распределена по нормальному закону. По выборке объёмом N=20 вычислены оценки математического ожидания и дисперсии . При заданной доверительной вероятности b найти предельную ошибку оценки математического ожидания и дисперсии. Определить, какими будут эти величины, если при выборке объёмом N=40 получены такие же величины оценок. Исходные величины следует взять из таблицы, приведенной ниже.

Последняя Цифра шифра	0	1	2	3	4	5	6	7	8	9
	-2	-3	-4	-1	-5	-4	-3	-2	-1	-6
S	0,8	0,9	0,7	0,6	0,3	0,5	0,4	1,1	1,2	1,3
Предпоследняя цифра шифра	0; 5	1; 6	2; 7	3; 8	4; 9
Доверительная Вероятность b	0,9	0,95	0,98	0,99	0,999

< Предыдущая		Следующая >