4.2.1. Лабораторная работа 1. Статистическое оценивание параметров плотности вероятности

Целью работы является изучение методики статистического оценивания параметров плотности вероятности, освоение инструментов системы MathCAD.

Порядок выполнения лабораторной работы

Лабораторная работа состоит из двух частей. Первая часть включает в себя выполнение заданий 1 и 2 и представляет собой контрольный пример, решение которого приведено ниже. Во второй части самостоятельно выполняется индивидуальное задание, включающее задания 3 и 4.

Задание 1

1.1. Получить с использованием системы MathCAD выборку объема N = 30 из генеральной совокупности, в которой случайная величина ξ имеет нормальную плотность вероятности с параметрами M = 0 и s = 2.

1.2. Найти точечные оценки математического ожидания, дисперсии, стандартного отклонения, а также стандартную ошибку оценки математического ожидания:

А) по данным малой выборки ;

Б) по данным большой выборки используя, возможности системы MathCAD.

Выполнение задания 1.1. Для выполнения задания необходимо запустить программу MathCAD, для чего следует в подменю Программы главного меню Пуск Панели задач найти группу MathSoft Apps, которая содержит пункт MathCAD 2000 Professional либо более старшие версии MathCAD, именно он и запускает саму программу MathCAD. Если на рабочем столе экрана присутствует ярлык MathCAD (MCAD в некоторых версиях), то запуск MathCAD осуществляется с рабочего стола щелчками левой клавиши мыши. На экране появится чистый рабочий лист, над которым находится панель управления, причем первая, третья и четвертая строки аналогичны строкам редактора Word, например строка меню с пунктами File,Edit И т. д. либо «Файл», «Правка» и т. д., если MathCAD руссифицирован, а также панель инструментов MathCAD во второй строке, содержащая различные меню: “Арифметика” для создания уравнений, меню простых операторов, меню создания графиков, меню работы с матрицами, меню для использования дифференциальных и интегральных соотношений, меню программирования, а также меню печати букв греческого алфавита. Четвертая строка панели служит для работы с текстами и позволяет печатать комментарии. Существует возможность загрузить ранее сохраненный рабочий лист, выбрав в меню File (Файл) Команду Open (Открыть). Курсор представляет собой маленький крестик (+), который легко можно перемещать с помощью мыши, для этого достаточно подвести указатель мыши в необходимое место и щелкнуть левой клавишей. Курсор определяет начало вставки объекта. MathCAD обрабатывает математические объекты слева направо, сверху вниз. Генерация случайных чисел с нормальной плотностью вероятности осуществляется с использованием функции «», где N – объем выборки, M – математическое ожидание, s – СКО. При обращении к этой функции образуется выборка случайных чисел Xi заданного объема, символ «:=» образуется при наборе символа «: », либо этот символ можно выбрать из меню простых операторов, индексация конкретного случайного числа образуется путем введения символа «[» после введения «Х». При этом следует учесть, что I Î [0,n-1] в силу специфики функции «Rnorm». Как видно из распечатки программы с комментариями на листе Документа 1, сначала задаются значения параметров N, M, s, после чего вводится функция «». Следует просмотреть некоторые значения выборки, используя выражение «Xi=», значение индекса I Необходимо задать конкретное. При введении символа «X=» система MathCAD выводит таблицу первых значений выборки и их номера, как это показано на странице, обозначенной как Документ 1. Для удаления ненужных символов в математических выражениях можно использовать клавишу [Bksp]. Для этого с помощью мыши курсор устанавливается правее символа, который нужно удалить. Нажав [Bksp], удаляем ненужный символ.

Выполнение задания 1.2. Задание 1.2 можно выполнить, если использовать оператор математического анализа на панели инструментов, обозначенный как (использование дифференциальных и интегральных соотношений), а также меню «Арифметика» и др. панели для ввода символов вида «S», «Ö», «/», возведение выражения в степень осуществляется с помощью символа «Ù». Формулы, используемые при выполнении задания 1.2, приведены в Документе 1, полученном путем распечатки программы MathCAD, снабженной соответствующими комментариями. Для ввода символов греческого алфавита используется меню «Символы греческого алфавита». При желании, для печати комментариев, можно использовать пункт меню «Вставка», далее «Текстовая область», после чего в текстовой рамке печатается комментарий. После набора текста вне текстовой рамки следует щелкнуть левой клавишей мыши, рамка исчезнет. Удаление символов осуществляется либо клавишей [Bksp] слева от курсора, либо [Del] справа от курсора. Оценка математического ожидания выборки может быть получена с использованием функции «Mean( )» MathCAD. Используя функцию «Var( )», можно получить асимптотически несмещенную оценку дисперсии выборки случайной величины.

Задание 2

Найти доверительные интервалы для оценок математического ожидания, полученного в задании 1.2, соответствующие доверительной вероятности

β = 0,95.

Выполнение задания 2. Задача о нахождении доверительного интервала для математического ожидания случайной величины с нормальной плотностью вероятности решена в примере, который рассмотрен в разделе 3 п. 3.4 опорного конспекта. В расчетах следует использовать вычисленные при выполнении задания 1 значения точечных оценок математического ожидания. В Документе 2 приведен пример расчета доверительного интервала.

Задание 3

3.1. Смоделировать выборку случайной величины ξ , с нормальной плотностью вероятности с параметрами и σ. Значения параметров и объема выборки следует выбрать в соответствии с последней цифрой шифра из табл.4.9 (случайное рассеивание возьмите равным предпоследней цифре шифра). Таблица 4.9

Послед-няя цифра шифра	0	1	2	3	4	5	6	7	8	9
,	1; 0,4	1;0,5	2;0,5	2; 0,4	3;0,5	3; 0,6	5; 0,6	6; 0,7	7; 0,6	8; 0,7
	30	29	28	27	30	29	28	27	30	29

3.2. Выполнить с использованием системы MathCAD точечное и интервальное оценивание математического ожидания генеральной совокупности по данным выборки, полученной в п. 3.1. Значение доверительной вероятности возьмите равным 0,90.

Задание 4

По результатам выполнения заданий 1 и 2 сформулировать и обосновать выводы о том, как изменяется точность найденных параметров в зависимости от объема выборки.

Просмотр отдельных значений выборки случайной величины:

Х15 = 0,138; х23 = -0,49; Х29 = 1.785.

Оценка математического ожидания выборки вычисляется по формуле:

M1 = 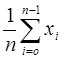, получим M1 = 0,17.

Оценка математического ожидания выборки с Использованием функции MathCad осуществляется командой M1 = Mean(X ). В результате получим значение M1 = 0,17, совпадающее с предыдущим значением.

Несмещенная оценка дисперсии и среднего квадратического отклонения выборки будут таковы:

D = 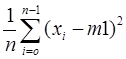, D = 2,84; σ = , σ = 1,685.

< Предыдущая		Следующая >