2.1.5. Плотность распределения Вероятности и ее свойства

Плотность распределения вероятностей F(X) удовлетворяет следующим свойствам.

1) В точках X непрерывности F(X) Имеет место равенство

. (2.12)

.

2) Для всех X Плотность распределения вероятностей неотрицательна, Т. е. .

3) Вероятность попадания Случайной величины в любой интервал [A,B] равна

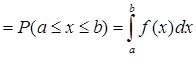. (2.13)

Это свойство означает, что удаление конечного числа точек из промежутка [A,B] не влияет на величину вероятности попадания в этот интервал.

4) Условие нормировки 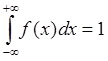. (2.14)

График Y=F(X) называют Кривой распределения. Графически свойство 3) Означает, что вероятность попадания случайной величины в интервал [A,B] численно равна площади S криволинейной трапеции, ограниченной сверху кривой распределения Y=F(X), снизу - осью OX, вертикальными прямыми X=A И X=B. Графически свойство 4) означает, что площадь криволинейной трапеции под всей кривой распределения Y=F(X) равна 1.

Вопросы для самопроверки

1. Какая величина называется дискретной случайной величиной?

2. Какую случайную величину называют непрерывной?

3. Что такое ряд распределения случайной величины?

4. Сформулируйте определение функции распределения случайной величины и ее свойства.

5. Что такое плотность вероятности случайной величины и ее свойства?

< Предыдущая		Следующая >