2.1.3. Непрерывные случайные величины

Кроме дискретных существуют непрерывные случайные величины. Примером непрерывной случайной величины является расстояние от точки попадания до центра мишени.

Определение. Случайная величина x называют Непрерывной, если ее значения целиком заполняют конечный или бесконечный интервал числовой оси.

Определение. Непрерывная случайная величина x называется Абсолютно непрерывной, Если существует такая функция F(X), Что для любых действительных чисел X Функция распределения этой случайной величины F(X) представима в виде 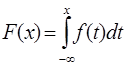, (2.7)

Т. е. функция распределения F(X) Этой случайной величины является интегралом с переменным пределом от F(X). Функция F(X) называется Плотностью распределения вероятностей случайной величины x такой, что

.

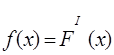Рассмотрим пример абсолютно непрерывной случайной величины.

Пример 2.5. Равномерное распределение.

Случайная величина ξ распределена Равномерно на промежутке [A,B], Если Ее плотность распределения вероятностей задается равенством

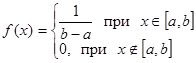
, (2.8)

Построим функцию распределения F(X) этой случайной величины, Используя равенство (2.7). При всех X<A По определению F(X) подынтегральная функция F(T)=0. Следовательно, функция распределения F(X)=0.

При всех A£ X <B по определению F(X) подынтегральная функция . Тогда из равенства (2.7) получаем

.

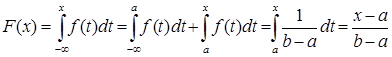При По свойству определенного интеграла и определению подынтегральной функции получаем следующее равенство

.

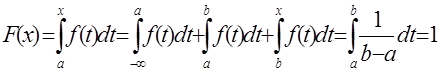Следовательно, функция распределения равномерного закона имеет вид:

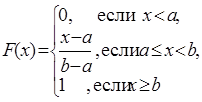. (2.9)

< Предыдущая		Следующая >