21. Поверхности второго порядка
Рассмотрим общее уравнение второго порядка относительно трех переменных:
![]() Где хотя бы один из коэффициентов A,B,C,D,E,F отличен от нуля.
Где хотя бы один из коэффициентов A,B,C,D,E,F отличен от нуля.
Поверхности, определяемые такими уравнениями, называются Поверхностями второго порядка.
Центром некоторой поверхности называется такая точка пространства, по отношению к которой точки этой поверхности расположены симметрично парами.
Поверхности второго порядка, обладающие единственным центром, называются Центральными.
Координаты центра ![]() такой поверхности определяются из системы (если она разрешима):
такой поверхности определяются из системы (если она разрешима):
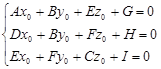
Поверхность, имеющая единственный центр, называется центральной. Центральными поверхностями второго порядка являются: эллипсоид, однополостный и двуполостный гиперболоид.
Канонические уравнения поверхностей второго порядка:
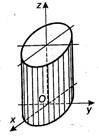
![]() - эллиптический цилиндр
- эллиптический цилиндр
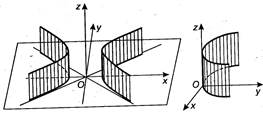
![]() - гиперболический цилиндр
- гиперболический цилиндр
![]() - параболический цилиндр
- параболический цилиндр
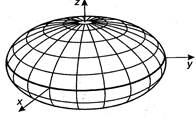
![]() - эллипсоид
- эллипсоид
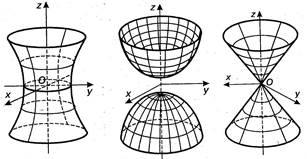
![]() - однополостный гиперболоид
- однополостный гиперболоид
![]() - двуполостный гиперболоид
- двуполостный гиперболоид
![]() - конус
- конус
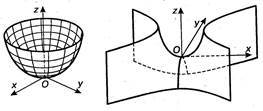
![]() - эллиптический параболоид
- эллиптический параболоид
![]() - гиперболический параболоид
- гиперболический параболоид
![]() - пара пересекающихся плоскостей
- пара пересекающихся плоскостей
![]() - пара параллельных плоскостей
- пара параллельных плоскостей
![]() - пара совпадающих плоскостей
- пара совпадающих плоскостей
| < Предыдущая | Следующая > |
|---|