20. Прямая в пространстве

Любая прямая в пространстве задается системой двух уравнений первой степени относительно трех переменных:

,

Т. е., прямую в пространстве можно задать, как линию пересечения двух непараллельных плоскостей.

Канонические уравнения.

Уравнения прямой проходящей через заданную точку Параллельно заданному (направляющему) вектору

Уравнения прямой, проходящей через две данные точки .

Параметрические уравнения.

Из канонических уравнений имеем:

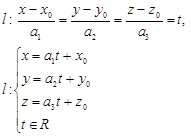
Если в качестве параметра принять время, то данные уравнения задают прямолинейное неускоренное движение со скоростью

Угол между прямыми в пространстве.

Пусть две прямые в пространстве заданы каноническими уравнениями:

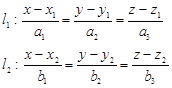
Тогда задача определения угла между этими прямыми сводится к определению угла между их направляющими векторами:

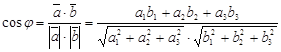
В частности, если ,

Если ,

Угол между прямой и плоскостью.

Пусть прямая задана каноническими уравнениями, а плоскость – общим уравнением

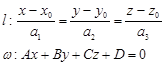
Соответственные направляющий и нормальный векторы:

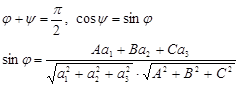
В частности, если ,

Если ,

< Предыдущая		Следующая >