19. Плоскость

Любая плоскость в пространстве задается уравнением первой степени относительно трех переменных и обратно: каждое такое уравнение задает на плоскости некоторую прямую.

- общее уравнение плоскости (где А, В,C одновременно не равны нулю).

Неполные уравнения:

- плоскость проходит через начало координат - плоскость параллельна оси Ox - плоскость параллельна оси Oy - плоскость параллельна оси Oz - плоскость параллельна плоскости Oxy - плоскость параллельна плоскости Oxz - плоскость параллельна плоскости Oyz - плоскость совпадает с плоскостью Oxy - плоскость совпадает с плоскостью Oxz - плоскость совпадает с плоскостью Oyz

Уравнение «в отрезках»:

Где M,N,P – длины отрезков, отсекаемых прямой на координатных осях

Каноническое.

Уравнение плоскости, проходящей через заданную точку Параллельно заданным неколлинеарным (направляющим) векторам

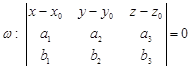
Уравнение плоскости, проходящей через три данные точки .

Параметрические уравнения.

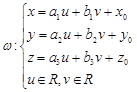
Уравнение плоскости, проходящей через данную точку перпендикулярно заданному вектору (вектору нормали)

Нормальное уравнение плоскости.

Где - углы, образованные вектором нормали с координатными осям, - Расстояние от начала координат до плоскости.

Взаимное расположение плоскостей.

Пусть плоскости заданы общими уравнениями:

Рассмотрим векторы нормали для этих плоскостей:

При и . В частности, при плоскости совпадают. Если двойное равенство не выполняется, то плоскости пересекаются под углом

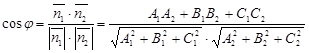
В частности, если ,

Расстояние от точки До плоскости

:

< Предыдущая		Следующая >