17. Линии на плоскости. Поверхности и линии в пространстве
Говорят, что уравнение F(X;Y)=0 задает на плоскости линию, если этому уравнению удовлетворяют координаты всех точек, лежащих на ней, и не удовлетворяют координаты точек, не лежащих на линии.
Пример: Уравнение ![]() задает на плоскости окружность с центром в точке
задает на плоскости окружность с центром в точке ![]() и радиуса R.
и радиуса R.
На практике линии могут задаваться также в полярных координатах, т. е. в виде ![]() или параметрическими уравнениями:
или параметрическими уравнениями:

Если в качестве параметра T принимать время, то параметрические уравнения определяют траекторию плоского движения точки.
Точку пересечения двух линий можно найти:
![]()
Говорят, что уравнение F(X;Y;Z)=0 задает в пространстве поверхность, если этому уравнению удовлетворяют координаты всех точек, лежащих на ней, и не удовлетворяют координаты точек, не лежащих на поверхности.
Пример: Уравнение ![]() задает в пространстве сферу с центром в точке
задает в пространстве сферу с центром в точке ![]() и радиуса R.
и радиуса R.
Поверхности в пространстве могут задаваться также параметрически:

Например, параметрические уравнения сферы радиуса R c центром в начале координат имеют вид:
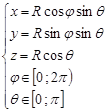
Линию в пространстве естественно рассматривать, как пересечение двух поверхностей:
![]()
Она может также задаваться также параметрическими уравнениями:

Если в качестве параметра T принимать время, то параметрические уравнения определяют координаты движущейся в пространстве материальной точки.
Для отыскания точек пересечения поверхностей или линий (или поверхности и линии) следует рассмотреть совместно уравнения, определяющие указанные геометрические объекты. Решение полученной при этом системы и определит координаты всех точек пересечения. Если полученная система не имеет решения, то точек пересечения объектов нет
| < Предыдущая | Следующая > |
|---|