16. Основные задачи аналитической геометрии на плоскости и в пространстве
1.Проекция направленного отрезка на ось.
Заметим, что проекция вектора на ось может принимать и отрицательное значение
2.Расстояние между точками.
А) На прямой
Б) На плоскости
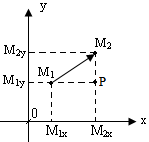
В)В пространстве аналогично:
3. Деление отрезков в данном отношении.
Говорят, что точка 
Делит отрезок 
в отношении , если 
Пусть 
и точка 
делит отрезок в заданном отношении .
Тогда координаты точки М:
В частности, при 
, точка M будет являться серединой данного отрезка и ее координаты вычисляются:
Заметим также, что при 
говорят, что точка М делит отрезок внешним образом.
Пример: Рассмотрим задачу о вычислении координат центра тяжести системы материальных точек 
. Сделаем следующие допущения:
с массами 
соответственно находится на отрезке 
и делит этот отрезок в отношении 
Центр тяжести системы точек 
с массами 
совпадает с центром тяжести системы из двух точек, одна из которых является точкой 
с массой 
, а другая находится в центре тяжести системы точек 
и имеет массу 
Тогда координаты центра тяжести системы точек 
вычисляются по формулам:
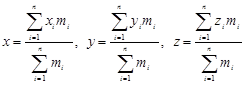
Полученные формулы используются для введения так называемых Барицентрических координат.
Рассмотрим на декартовой плоскости три различные точки 
, не лежащие на одной прямой и фиксированную точку 
. Выясним, существуют ли такие три числа 
, удовлетворяющие условию 
, что данная точка 
будет являться центром тяжести системы трех данных точек 
С массами 
соответственно. Можно показать, что для каждой точки 
эти числа определяются однозначно из системы:
Числа 
называются Барицентрическими координатами точки М относительно базисных точек 
В пространстве барицентрические координаты вводятся аналогично. Для этого используются четыре базисные точки, не лежащие в одной плоскости.
| < Предыдущая | Следующая > |
|---|
