18. Прямая на плоскости

Любая прямая на плоскости задается уравнением первой степени относительно двух переменных и обратно: каждое такое уравнение задает на плоскости некоторую прямую.

- общее уравнение прямой (где А, В одновременно не равны нулю).

Неполные уравнения:

- прямая проходит через начало координат - прямая параллельна оси Ox - прямая параллельна оси ОY

Уравнение «в отрезках»:

Где M,N – длины отрезков, отсекаемых прямой на координатных осях

Каноническое.

Уравнение прямой, проходящей через заданную точку Параллельно заданному (направляющему) вектору

Уравнение прямой, проходящей через две данные точки .

Параметрические уравнения.

Из канонического уравнения имеем:

Если в качестве параметра принять время, то данные уравнения задают прямолинейное неускоренное движение со скоростью

Уравнение прямой, проходящей через точку с заданным угловым коэффициентом K.

Уравнение прямой, проходящей через данную точку перпендикулярно заданному вектору (вектору нормали)

Нормальное уравнение прямой.

Взаимное расположение прямых.

Пусть прямые заданы общими уравнениями:

Рассмотрим векторы нормали для этих прямых:

При и . В частности, при прямые совпадают. Если , то прямые пересекаются под углом

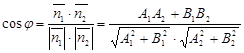
В частности, если ,

Расстояние от точки До прямой :

19.Кривые второго порядка.

Общим уравнением второго порядка называется уравнение вида:

Где коэффициенты A,B,C одновременно не равны нулю.

Линии, определяемые такими уравнениями, называются Кривыми второго порядка.

Центром некоторой линии называется такая точка плоскости, по отношению к которой точки этой линии расположены симметрично парами.

Линии второго порядка, обладающие единственным центром, называются Центральными.

Координаты центра линии определяются из системы:

Обозначим через .

При кривая второго порядка будет центральной.

Причем, при уравнение является уравнением Эллиптического типа. Каждое эллиптическое уравнение является уравнением либо обыкновенного эллипса, либо вырожденного эллипса (точка), либо мнимого эллипса (в этом случае уравнение не определяет на плоскости никакого геометрического образа).

При уравнение является уравнением Гиперболического типа. Каждое гиперболическое уравнение определяет либо обыкновенную гиперболу, либо вырожденную (пару пересекающихся прямых).

При Линия второго порядка не является центральной. Такие уравнения называются уравнениями Параболического типа и определяют на плоскости либо обыкновенную параболу, либо пару параллельных (или совпадающих) прямых, либо не определяют на плоскости никакого геометрического образа

< Предыдущая		Следующая >